Advertisements
Advertisements
Question
आकुति में, छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
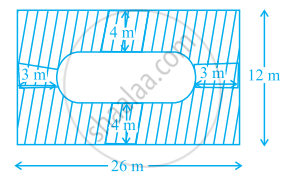
Solution
GH और FE को ऐसे मिलाएँ कि EFGH आयत हो।
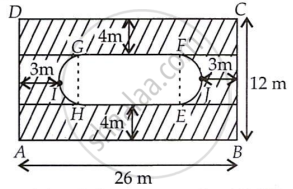
यहाँ, आयत ABCD की चौड़ाई = BC = 12 m
∴ आंतरिक आयत EFGH की चौड़ाई = EF
= [12 – (4 + 4)] m
= 4 m
जो अर्ध-वृत्त के व्यास EJF = 4 m के बराबर है।
∴ अर्ध-वृत्त EJF की त्रिज्या, (r) = 2 m
आंतरिक आयत EFGH की लंबाई = EH
= [26 – (5 + 5)] m
= 16 m
∴ दो अर्ध-वृत्त EJF और HIG का क्षेत्रफल
= `2((π"r"^2)/2)`
= `2 xx (π(2)^2)/2 "m"^2`
= 4π m2
अब, आंतरिक आयत EFGH का क्षेत्रफल
= EH × EF
= (16 × 4) m2
= 64 m2
और बाहरी आयत ABCD का क्षेत्रफल
= (26 × 12) m2
= 312 m2
∴ छायांकित क्षेत्र का क्षेत्रफल = बाहरी आयत का क्षेत्रफल – (दो अर्धवृत्तों का क्षेत्रफल + आंतरिक आयत का क्षेत्रफल)
= [312 – (4π + 64)] m2
= (248 – 4π) m2
APPEARS IN
RELATED QUESTIONS
भुजा 4 सेमी वाले एक वर्ग के प्रत्येक कोने से 1 सेमी त्रिज्या वाले वृत्त का एक चतुर्थांश काटा गया है तथा बीच में 2 सेमी व्यास का एक वृत भी काटा गया है, जैसा कि आकृति में दर्शाया गया है। वर्ग के शेष भाग का क्षेत्रफल ज्ञात कीजिए। [उपयोग Π = `22/7`]

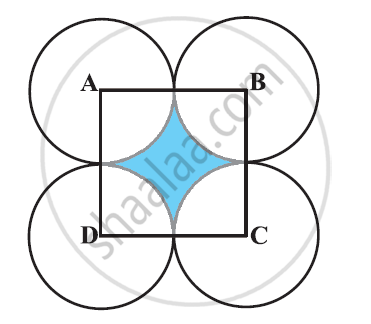
दी गई आकृति में, ABCD भुजा 14 सेमी वाला एक वर्ग है। A, B, C और D को केंद्र मानकर, चार वृत्त इस प्रकार खींचे गए हैं कि प्रत्येक वृत्त तीन शेष वृत्तों में दो वृत्तों को बाह्य रूप से स्पर्श करता है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। [उपयोग Π = 22/7]
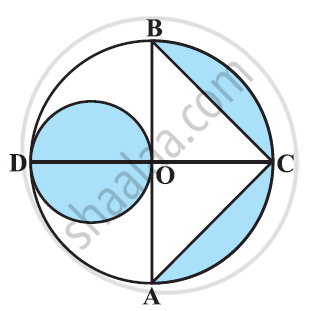
दी गई आकृति में AB और CD केंद्र O वाले एक वृत्त के दो परस्पर लंब व्यास हैं तथा OD छोटे वृत्त का व्यास है। यदि OA = 7 सेमी है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। [उपयोग Π = `22/7`]
एक समबाहु त्रिभुज ABC का क्षेत्रफल 17320.5 वर्ग सेमी है। भुजा के आधे के बराबर की त्रिज्या लेकर एक वृत्त खींचा जाता है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। [Use π = 3.14 and `sqrt3 `= 1.73205]

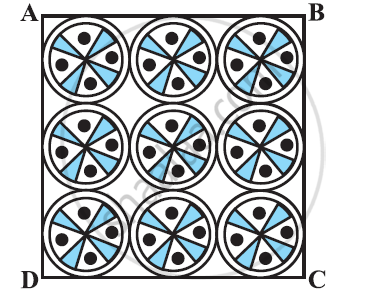
एक वर्गाकार रूमाल पर, नौ वृत्ताकार डिजाइन बने हैं, जिनमें से प्रत्येक की त्रिज्या 7 सेमी है। रूमाल के शेष भाग का क्षेत्रफल ज्ञात कीजिए।
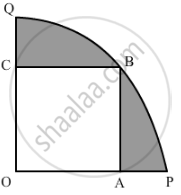
दी गई आकृति में, एक चतुर्थांश OPBQ के अंतर्गत एक वर्ग OABC बना हुआ है। यदि OA = 20 सेमी है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। (Use π = 3.14)
दी गई आकृति में, ABC त्रिज्या 12 सेमी वाले एक वृत का चतुर्थांश है तथा BC को व्यास मानकर एक अर्धवृत्त्त खींचा गया है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। [उपयोग Π = 22/7]

दी गई आकृति में छायांकित डिजाइन का क्षेत्रफल ज्ञात कीजिए, जो 8 सेमी त्रिज्याओं वाले दो वृत्तों के चतुर्थांशों के बीच उभयनिष्ठ है। [उपयोग Π = 22/7]

त्रिज्या 8 cm वाले एक वृत्त के अंतर्गत खींचे जा सकने वाले वर्ग का क्षेत्रफल ______ है।
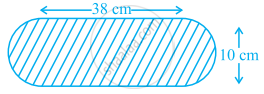
आकृति में दर्शायी गयी फूलों की क्यारी (अर्धवृत्ताकार सिरों वाली) का क्षेत्रफल ज्ञात कीजिए।