Advertisements
Advertisements
Question
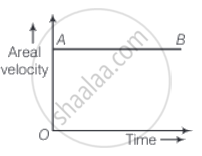
Draw areal velocity versus time graph for mars.
Solution
The areal velocity of a planet revolving around the sun is constant with time. Therefore, the graph between areal velocity and time is a straight line (AB) parallel to the time axis. ( Kepler's second law).
APPEARS IN
RELATED QUESTIONS
State Kepler's law of orbit and law of equal areas.
A comet orbits the Sun in a highly elliptical orbit. Does the comet have a constant (a) linear speed, (b) angular speed, (c) angular momentum, (d) kinetic energy, (e) potential energy, (f) total energy throughout its orbit? Neglect any mass loss of the comet when it comes very close to the Sun.
A Saturn year is 29.5 times the earth year. How far is the Saturn from the sun if the earth is 1.50 ×108 km away from the sun?
Let the period of revolution of a planet at a distance R from a star be T. Prove that if it was at a distance of 2R from the star, its period of revolution will be \[\sqrt{8}\] T.
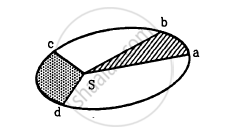
In the Following figure shows the elliptical path of a planet about the sun. The two shaded parts have equal area. If t1 and t2 be the time taken by the planet to go from a to b and from c to d respectively,
Observe the given figure showing the orbit of a planet moving around the Sun and write the three laws related to it:

The orbit of a planet moving around the Sun
Supposing Newton’s law of gravitation for gravitation forces F1 and F2 between two masses m1 and m2 at positions r1 and r2 read F1 = – F2 = `- r_12/r_12^3 GM_0^2 ((m_1m_2)/M_0^2)^n` where M0 is a constant of dimension of mass r12 = r1 – r2 and n is a number. in such a case.
- the acceleration due to gravity on earth will be different for different objects.
- none of the three laws of Kepler will be valid.
- only the third law will become invalid.
- for n negative, an object lighter than water will sink in water.
A satellite is in an elliptic orbit around the earth with aphelion of 6R and perihelion of 2 R where R= 6400 km is the radius of the earth. Find eccentricity of the orbit. Find the velocity of the satellite at apogee and perigee. What should be done if this satellite has to be transferred to a circular orbit of radius 6R ?
[G = 6.67 × 10–11 SI units and M = 6 × 1024 kg]
The maximum and minimum distances of a comet from the Sun are 1.6 × 1012 m and 8.0 × 1010 m respectively. If the speed of the comet at the nearest point is 6 × 104 ms-1, the speed at the farthest point is ______.
lf the angular momentum of a planet of mass m, moving around the Sun in a circular orbit is L, about the center of the Sun, and its areal velocity is ______.
