Advertisements
Advertisements
Question
Draw a schematic sketch of an ac generator describing its basic elements. State briefly its working principle. Show a plot of variation of
(i) Magnetic flux and
(ii) Alternating emf versus time generated by a loop of wire rotating in a magnetic field.
Solution
Principle − Based on the phenomenon of electromagnetic induction.
Construction:

Main parts of an ac generator:
Armature − The rectangular coil ABCD
Filed Magnets − Two pole pieces of a strong electromagnet
Slip Rings − The ends of the coil ABCD are connected to two hollow metallic rings R1 and R2.
Brushes − B1 and B2 are two flexible metal plates or carbon rods. They are fixed and are kept in tight contact with R1 and R2, respectively.
Working − As the armature coil is rotated in the magnetic field, angle θ between the field and the normal to the coil changes continuously. Therefore, magnetic flux linked with the coil changes and an emf is induced in the coil. According to Fleming’s right hand rule, current is induced from A to B in AB and from C to D in CD. In the external circuit, current flows from B2 to B1.
To calculate the magnitude of emf induced:
Suppose A → Area of each turn of the coil
N → Number of turns in the coil
`vecB`→ Strength of the magnetic field
θ → Angle which normal to the coil makes with `vecB` at any instant t
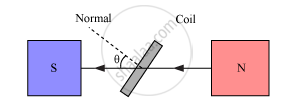
∴ Magnetic flux linked with the coil in this position is given by,
`phi=N(vecB.vecA)=NBAcostheta=NBAcos `
Where, ‘ω’ is angular velocity of the coil
Graph between magnetic flux and time, according to equation (i), is shown below:

As the coil rotates, angle θ changes. Therefore, magnetic flux Φ linked with the coil changes and an emf is induced in the coil. At this instant t, if e is the emf induced in the coil, then
`e=(dtheta)/dt=-d/dt(NABcos`
`=-NABd/dt(cos `
=-NAB(-sin ωt)ω
∴ e = NAB ω sin ωt
The graph between alternating emf versus time is shown below:

APPEARS IN
RELATED QUESTIONS
The current flowing through an inductor of self inductance L is continuously increasing. Plot a graph showing the variation of
Magnetic flux versus the current
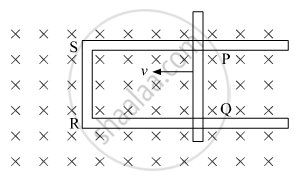
Figure shows a rectangular loop conducting PQRS in which the arm PQ is free to move. A uniform magnetic field acts in the direction perpendicular to the plane of the loop. Arm PQ is moved with a velocity v towards the arm Rs. Assuming that the arms QR, RS and SP have negligible resistances and the moving arm PQ has the resistance r, obtain the expression for (i) the current in the loop (ii) the force and (iii) the power required to move the arm PQ.
Whenever the magnetic flux linked with an electric circuit changes, an emf is induced in the circuit. This is called ______.
The unit of magnetic flux in SI is ______
The dimensional formula of magnetic flux is ______.
A loop, made of straight edges has six corners at A(0, 0, 0), B(L, O, 0) C(L, L, 0), D(0, L, 0) E(0, L, L) and F(0, 0, L). A magnetic field `B = B_o(hati + hatk)`T is present in the region. The flux passing through the loop ABCDEFA (in that order) is ______.
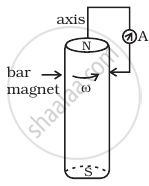
A cylindrical bar magnet is rotated about its axis (Figure). A wire is connected from the axis and is made to touch the cylindrical surface through a contact. Then
A circular coil of 1000 turns each with area 1 m2 is rotated about its vertical diameter at the rate of one revolution per second in a uniform horizontal magnetic field of 0.07T. The maximum voltage generation will be ______ V.
The Figure below shows an infinitely long metallic wire YY' which is carrying a current I'.
P is a point at a perpendicular distance r from it.
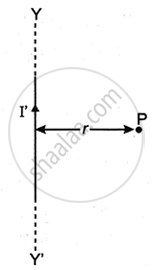
- What is the direction of magnetic flux density B of the magnetic field at the point P?
- What is the magnitude of magnetic flux density B of the magnetic field at the point P?
- Another metallic wire MN having length l and carrying a current I is now kept at point P. If the two wires are in vacuum and parallel to each other, how much force acts on the wire MN due to the current I' flowing in the wire YY'?
