Advertisements
Advertisements
Question
Draw the graphs of the following linear equations on the same graph paper.
2x + 3y = 12, x – y = 1.
Find the co-ordinates of the vertices of the triangle formed by the two straight lines and the y-axis. Also, find the area of the triangle.
Solution
The given equations are:
2x + 3y = 12
x – y = 1
To graphically represent the above equations, we need at least two solutions for each equation.
For equation 2x + 3y = 12,
3y = 12 − 2x
y = `(12 − 2x)/3`
`"If x = 0, then y"= [12 − 2(0)]/3 = [12 − 0]/3 = 12/3 = 4`
`"If x = 3, then y"= [12 − 2(3)]/3 = [12 − 6]/3 = 6/3 = 2`
| x | 0 | 3 |
| y | 4 | 2 |
For equation x − y = 1,
y = x − 1
If x = 0, then y = 0 − 1 = − 1
If x = 3, then y = 3 − 1 = 2
| x | 0 | 3 |
| y | −1 | 2 |
The equation of y-axis is x = 0.
The following graph depicts the above situation:

The lines AB, CD and AC represent the equations 2x + 3y = 12, x − y = 1 and y-axis respectively.
As we can see, the vertices of the given triangle are the points of intersection of the lines AB, CD, and AC taken in pairs.
We know that,
Area of ΔABC = `1/2` × Base × Height
The height of the triangle in the graph represents the distance between point B and the y-axis.
Height of the triangle = 3 units.
AC's base equals the distance between points A and C.
Base of the triangle = 4 + 1 = 5 units.
Area of the triangle formed by the given lines = `1/2` × 5 × 3 = 7.5 sq. units.
APPEARS IN
RELATED QUESTIONS
From the choices given below, choose the equation whose graph is given in fig. below.
(i) y = x + 2 (ii) y = x – 2 (iii) y = −x + 2 (iv) x + 2y = 6
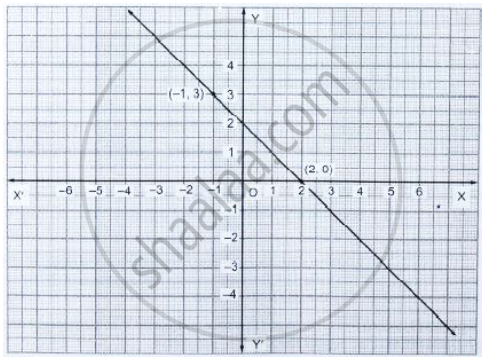
[Hint: Clearly, (2, 0) and (−1, 3) satisfy the equation y = −x + 2]
Draw the graph for the equation, given below :
x - 5y + 4 = 0
Solve, graphically, the following pairs of equation :
x - 5 = 0
y + 4 = 0
Solve, graphically, the following pairs of equation :
3x + 7y = 27
8 - y = `(5)/(2)x`
Use graph paper for this question. Take 2 cm = 1 unit on both the axes.
- Draw the graphs of x + y + 3 = 0 and 3x - 2y + 4 = 0. Plot only three points per line.
- Write down the coordinates of the point of intersection of the lines.
- Measure and record the distance of the point of intersection of the lines from the origin in cm.
Draw the graph for each of the following equation: Also, find the coordinates of the points where the graph of the equation meets the coordinate axes:
`(3x + 14)/(2) = (y - 10)/(5)`
Draw the graph of the equation
y = 5x - 4 Find graphically
a. the value of x, when y = 1
b. the value of y, when x = -2
Draw the graph for the following
3x + 2y = 14
Find the values.
y = 3x + 1
| x | − 1 | 0 | 1 | 2 |
| y |
The following observed values of x and y are thought to satisfy a linear equation. Write the linear equation:
| x | 6 | – 6 |
| y | –2 | 6 |
Draw the graph using the values of x, y as given in the above table. At what points the graph of the linear equation cuts the y-axis
