Advertisements
Advertisements
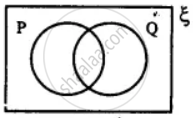
Question
Draw the Venn diagrams to illustrate the following relationship among sets E, M and U, where E is the set of students studying English in a school, M is the set of students studying Mathematics in the same school, U is the set of all students in that school.
Some of the students study Mathematics but do not study English, some study English but do not study Mathematics, and some study both.
Solution
Since there are some students who study both English and Mathematics, some English only and some Mathematics only.
Thus, the Venn Diagram is
APPEARS IN
RELATED QUESTIONS
Draw a Venn diagram for the truth of the following statement :
All rational number are real numbers.
Draw Venn diagram for the truth of the following statements :
Some rectangles are squares.
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[A \cup B\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[A \cap \left( B \cup C \right)\]
Let \[A = \left\{ x: x \in N \right\}, B = \left\{ x: x - 2n, n \in N \right\}, C = \left\{ x: x = 2n - 1, n \in N \right\}\]and D = {x : x is a prime natural number}. Find: \[A \cap B\]
Let \[A = \left\{ x: x \in N \right\}, B = \left\{ x: x - 2n, n \in N \right\}, C = \left\{ x: x = 2n - 1, n \in N \right\}\] and D = {x : x is a prime natural number}. Find: \[A \cap D\]
Let A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}. Find: \[C - A\]
- show the sets U, P and P' by the Venn diagram.
- Verify (P')' = P
Represent the union of two sets by Venn diagram for the following.
Y = {y | y is an odd number between 90 and 100}
Using the Venn diagram, examine the logical equivalence of the following statements:
(a) Some politicians are actors.
(b) There are politicians who are actors.
(c) There are politicians who are not actors.
From the given diagram find :
A ∪ B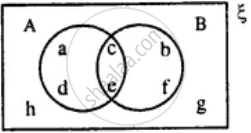
From the given diagram find :
B - A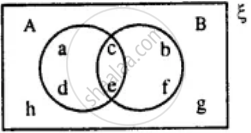
Use the given Venn-diagram to find:
B - A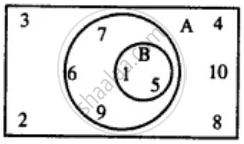
Draw a Venn-diagram to show the relationship between two overlapping sets A and B. Now shade the region representing :
A ∪ B
Draw a Venn-diagram to show the relationship between two sets A and B; such that A ⊆ B, Now shade the region representing :
A ∪ B
Draw a Venn-diagram to show the relationship between two sets A and B; such that A ⊆ B, Now shade the region representing :
A ∩ B
Draw a Venn-diagram to show the relationship between two sets A and B; such that A ⊆ B, Now shade the region representing :
(A ∪ B)'
Two sets A and B are such that A ∩ B = Φ. Draw a venn-diagram to show the relationship between A and B. Shade the region representing :
A ∪ B
In the given diagram, shade the region which represents the set given underneath the diagrams: (A ∩ B)'
In the given diagram, shade the region which represents the set given underneath the diagrams: (P ∩ Q)'
From the given diagram, find :
(i) (A ∪ B) - C
(ii) B - (A ∩ C)
(iii) (B ∩ C) ∪ A
Verify :
A - (B ∩ C) = (A - B) ∪ (A - C)

Represent the truth of the following statement by the Venn diagram.
All teachers are scholars and scholars are teachers.
Express the truth of the following statement by the Venn diagram.
All men are mortal.
Express the truth of the following statement by the Venn diagram.
No child is an adult.
Draw the Venn diagrams to illustrate the following relationship among sets E, M and U, where E is the set of students studying English in a school, M is the set of students studying Mathematics in the same school, U is the set of all students in that school.
There is no student who studies both Mathematics and English.
Draw the Venn diagrams to illustrate the following relationship among sets E, M and U, where E is the set of students studying English in a school, M is the set of students studying Mathematics in the same school, U is the set of all students in that school.
Not all students study Mathematics, but every students studying English studies Mathematics.
