Advertisements
Advertisements
Question
एक यातायात संकेत बोर्ड पर 'आगे स्कूल है’ लिखा है और यह भुजा ‘a‘ वाले एक समबाहु त्रिभुज के आकार का है। हीरोन के सूत्र का प्रयोग करके इस बोर्ड का क्षेत्रफल ज्ञात कीजिए। यदि संकेत बोर्ड का परिमाप 180 cm है, तो इसका क्षेत्रफल क्या होगा?
Solution
यातायात संकेत बोर्ड की भुजा = a
यातायात संकेत बोर्ड का परिमाप = 3 × a
2s = 3a ⇒ s = `3/2 a`
हीरोन के सूत्र से,
त्रिभुज का क्षेत्रफल = `sqrt(s(s-a)(s-b)(s-c))`
दिए गए त्रिभुज का क्षेत्रफल = `sqrt(3/2 a(3/2a-a)(3/2a-a)(3/2a-a))`
= `sqrt((3/2a)(a/2)(a/2)(a/2))`
= `sqrt3/4a^2` ...(1)
यातायात संकेत बोर्ड का परिमाप = 180 cm
यातायात संकेत बोर्ड की भुजा (a) = `(180/3) cm` = 60 cm
समीकरण (1) का उपयोग करते हुए, यातायात संकेत बोर्ड का क्षेत्रफल
= `sqrt3/4(60cm)^2`
= `(3600/4sqrt3)cm^2` = `900sqrt3 cm^2`
APPEARS IN
RELATED QUESTIONS
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी दो भुजाएँ 18 cm और 10 cm हैं तथा उसका परिमाप 42 cm है।
एक त्रिभुज की भुजाओं का अनुपात 12 : 17 : 25 है और उसका परिमाप 540 cm है। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
एक त्रिभुज की भुजाएँ 35 cm, 54 cm और 61 cm की हैं। इसके सबसे लंबे शीर्षलंब की लंबाई है
एक त्रिभुज ABC का क्षेत्रफल 8 cm2 है, जिसमें AB = AC = 4 cm है तथा ∠A = 90° है।
भुजा a वाले एक समषड्भुज का क्षेत्रफल भुजा a वाले पाँच समबाहु त्रिभुजों के क्षेत्रफलों के योग के बराबर होता है।
एक त्रिभुजाकार मैदान जिसकी भुजाएँ 51 m, 37 m और 20 m हैं को 3 रु. प्रति m2 की दर से समतल कराने का व्यय 918 रु है।
एक समबाहु त्रिभुज के अभ्यंतर में स्थित किसी बिंदु से तीनों भुजाओं पर लंब डाले जाते हैं। इन लंबों की लंबाई 14 cm, 10 cm और 6 cm हैं। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
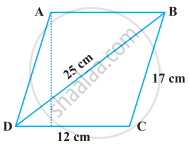
आकृति में दिए हुए समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए। साथ ही, शीर्ष A से भुजा DC पर शीर्षलंब की लंबाई ज्ञात कीजिए।
एक त्रिभुजाकार खेत का परिमाप 420 m है तथा इसकी भुजाओं का अनुपात 6 : 7 : 8 है। इस खेत का क्षेत्रफल ज्ञात कीजिए।
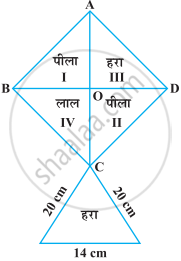
निम्नलिखित आकृति में दी हुई पतंग को बनाने के लिए प्रत्येक शेड (रंग) के कितने कागज की आवश्यकता होगी, यदि ABCD विकर्ण 44 cm वाला एक वर्ग है।