Advertisements
Advertisements
Question
एक समबाहु त्रिभुज के अभ्यंतर में स्थित किसी बिंदु से तीनों भुजाओं पर लंब डाले जाते हैं। इन लंबों की लंबाई 14 cm, 10 cm और 6 cm हैं। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
Solution
मान लीजिए ABC एक समबाहु त्रिभुज है और O आंतरिक बिंदु है तथा AQ, BR और CP बिंदु O से खींचे गए लंब हैं जिससे OQ = 10 cm, OR = 6 cm, OP = 14 cm है।
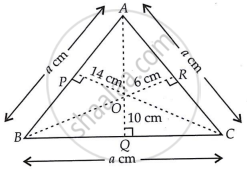
मान लीजिए एक समबाहु त्रिभुज की भुजाएँ a cm हैं।
ΔOAB का क्षेत्रफल = `1/2 xx AB xx OP`
= `(1/2 xx a xx 14)cm^2`
= 7a cm2 ...(i)
ΔOBC का क्षेत्रफल = `1/2 xx BC xx OQ`
= `(1/2 xx a xx 10)cm^2`
= 5a cm2 ...(ii)
ΔOAC का क्षेत्रफल = `1/2 xx AC xx OR`
`(1/2 xx a xx 6)cm^2`
= 3a cm2 ...(iii)
∴ ΔABC का क्षेत्रफल = (ΔOAB + ΔOBC + ΔOAC) का क्षेत्रफल
= (7a + 5a + 3a) cm2
= 15a cm2 ...(iv) [From (i), (ii) and (iii)]
समबाहु ΔABC का क्षेत्रफल = `sqrt(3)/4 a^2` ...(v)
(iv) और (v) से,
`sqrt(3)/4 a^2 = 15a`
`\implies a = (60sqrt(3))/3 = 20sqrt(3)`
(v) में `a = 20sqrt(3)` प्रतिस्थापित करने पर, हमें प्राप्त होता है।
ΔABC का क्षेत्रफल = `sqrt(3)/4 (20sqrt(3))^2`
= `300sqrt(3)`
इस प्रकार, एक समबाहु त्रिभुज का क्षेत्रफल `300sqrt(3) cm^2` है।
APPEARS IN
RELATED QUESTIONS
एक यातायात संकेत बोर्ड पर 'आगे स्कूल है’ लिखा है और यह भुजा ‘a‘ वाले एक समबाहु त्रिभुज के आकार का है। हीरोन के सूत्र का प्रयोग करके इस बोर्ड का क्षेत्रफल ज्ञात कीजिए। यदि संकेत बोर्ड का परिमाप 180 cm है, तो इसका क्षेत्रफल क्या होगा?
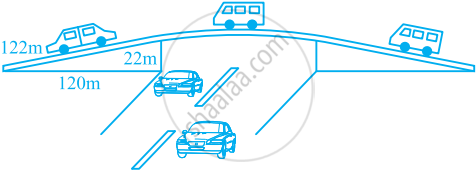
किसी फ्लाईओवर (Flyover) की त्रिभुजाकार दीवार को विज्ञापनों के लिए प्रयोग किया जाता है। दीवार की भुजाओं की लंबाइयाँ 122 m, 22 m और 120 m हैं (देखिए आकृति)। इस विज्ञापन से प्रति वर्ष ₹ 5000 प्रति m2 की प्राप्ति होती है। एक कंपनी ने एक दीवार को विज्ञापन देने के लिए 3 महीने के लिए किराए पर लिया। उसने कुल कितना किराया दिया?
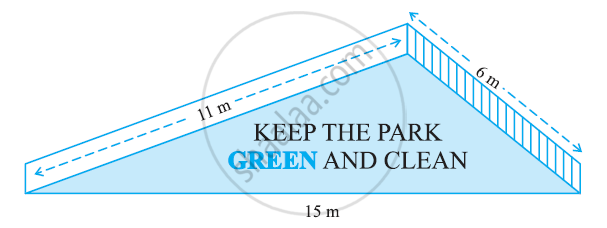
किसी पार्क में एक फिसल पट्टी (Slide) बनी हुई है। इसकी पार्श्वीय दीवारों (Side Walls) में से एक दीवार पर किसी रंग से पेंट किया गया है और उस पर ‘‘पार्क को हरा-भरा और साफ़ रखिए” लिखा हुआ है। (देखिए आकृति)। यदि इस दीवार की विमाएँ 15 m, 11 m और 6 m हैं, तो रंग से पेंट हुए भाग का क्षेत्रफल ज्ञात कीजिए।
एक समद्विबाहु त्रिभुज का परिमाप 30 cm है और उसकी बराबर भुजाएँ 12 cm लंबाई की हैं। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
`2sqrt(3)` cm भुजा वाले समबाहु त्रिभुज का क्षेत्रफल है
एक समबाहु त्रिभुज का क्षेत्रफल `20sqrt(3)` cm2 है, जिसकी प्रत्येक भुजा 8 cm है।
एक समांतर चतुर्भुज का आधार और संगत शीर्षलंब क्रमश : 10 cm और 3.5 cm हैं। उस समांतर चतुर्भुज का क्षेत्रफल 30 cm2 है।
भुजा a वाले एक समषड्भुज का क्षेत्रफल भुजा a वाले पाँच समबाहु त्रिभुजों के क्षेत्रफलों के योग के बराबर होता है।
एक समचतुर्भुज के आकार की शीट (चादर), जिसका परिमाप 40 cm और एक विकर्ण 12 cm है, को दोनों ओर से 5 रु प्रति m2 की दर से पेंट किया जाता है। पेंट करवाने की लागत ज्ञात कीजिए।
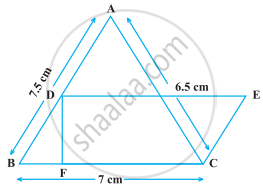
निम्नलिखित आकृति में, ∆ABC की भुजाओं में AB = 7.5 cm, AC = 6.5 cm और BC = 7 cm है। आधार BC पर एक समांतर चतुर्भुज DBCE की रचना की जाती है, जो क्षेत्रफल में ∆ABC के बराबर है। इस समांतर चतुर्भुज की ऊँचाई DF ज्ञात कीजिए।