Advertisements
Advertisements
Question
एक समचतुर्भुज के आकार की शीट (चादर), जिसका परिमाप 40 cm और एक विकर्ण 12 cm है, को दोनों ओर से 5 रु प्रति m2 की दर से पेंट किया जाता है। पेंट करवाने की लागत ज्ञात कीजिए।
Solution
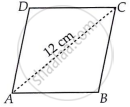
मान लीजिए ABCD एक समचतुर्भुज है जिसकी भुजाएँ AB = BC = CD = DA = x cm हैं।
दिया है कि एक समचतुर्भुज का परिमाप = 40 cm
`\implies` x + x + x + x = 40
`\implies` 4x = 40
`\implies x = 40/4`
∴ x = 10
ΔABC में, मान लीजिए a = AB = 10 cm, b = BC = 10 cm और c = AC = 12 cm
अब, ΔABC का अर्ध-परिमाप,
`s = (a + b + c)/2`
= `((10 + 10 + 12)/2) cm`
= `32/2 cm`
= 16 cm
∴ ΔABC का क्षेत्रफल = `sqrt(s(s - a)(s - b)(s - c))`
= `sqrt(16(16 - 10)(16 - 10)(16 - 12)) cm^2`
= `sqrt(16 xx 6 xx 6 xx 4) cm^2`
= 48 cm2
अब, समचतुर्भुज ABCD का क्षेत्रफल
= 2(ΔABC का क्षेत्रफल)
= (2 × 48) cm2
= 96 cm2
∵ 1 cm2 की शीट को पेंट करने की लागत = रु. 5
∴ 96 cm2 की शीट को पेंट करने की लागत
= रु. (96 × 5)
= रु. 480
अत:, शीट को दोनों तरफ से रंगने का व्यय = रु. (2 × 480) = रु. 960
APPEARS IN
RELATED QUESTIONS
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी दो भुजाएँ 18 cm और 10 cm हैं तथा उसका परिमाप 42 cm है।
एक त्रिभुज की भुजाओं का अनुपात 12 : 17 : 25 है और उसका परिमाप 540 cm है। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
एक समद्विबाहु त्रिभुज का परिमाप 30 cm है और उसकी बराबर भुजाएँ 12 cm लंबाई की हैं। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
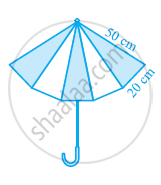
दो विभिन्न रंगों के कपड़ों के 10 त्रिभुजाकार टुकड़ों की सिलाई करके एक छाता बनाया गया है (देखिए आकृति) प्रत्येक टुकड़े के माप 20 सेमी, 50 सेमी और 50 सेमी हैं। छाते में प्रत्येक रंग का कितना कपड़ा लगा है?
यदि एक समचतुर्भुज की एक भुजा 10 cm और एक विकर्ण 16 cm है, तो उस समचतुर्भुज का क्षेत्रफल 96 cm2 है।
एक समांतर चतुर्भुज का आधार और संगत शीर्षलंब क्रमश : 10 cm और 3.5 cm हैं। उस समांतर चतुर्भुज का क्षेत्रफल 30 cm2 है।
एक त्रिभुजाकार मैदान जिसकी भुजाएँ 51 m, 37 m और 20 m हैं को 3 रु. प्रति m2 की दर से समतल कराने का व्यय 918 रु है।
भुजाओं 50 m, 65 m और 65 m वाले त्रिभुजाकार खेत में 7 रु. प्रति m2 की दर से घास लगवाने का व्यय ज्ञात कीजिए।
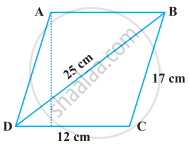
आकृति में दिए हुए समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए। साथ ही, शीर्ष A से भुजा DC पर शीर्षलंब की लंबाई ज्ञात कीजिए।
एक त्रिभुजाकार खेत का परिमाप 420 m है तथा इसकी भुजाओं का अनुपात 6 : 7 : 8 है। इस खेत का क्षेत्रफल ज्ञात कीजिए।
