Advertisements
Advertisements
Question
निम्नलिखित आकृति में दी हुई ऊँचाई PQ वाले समलंब PORS का क्षेत्रफल ज्ञात कीजिए।
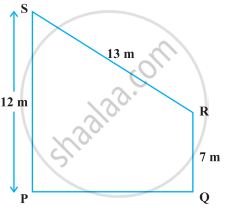
Solution
हमारे पास एक समलम्ब PQRD है, जिसमें PS पर एक लंब RT रेखा खींची गई है।
जहाँ, भुजा ST = PS – TP = 12 – 7 = 5 m। ...[∵ TP = PQ = 7 m]
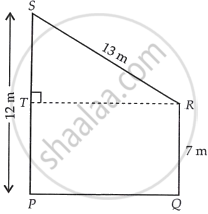
समकोण ΔSTR में,
(SR)2 = (ST)2 + (TR)2 ...[पाइथागोरस प्रमेय का उपयोग करके]
⇒ (13)2 = (5)2 + (TR)2
⇒ (TR)2 = 169 – 25
⇒ (TR)2 = 144
∴ TR = 12 m ...[सकारात्मक वर्गमूल लेने पर क्योंकि लम्बाई हमेशा धनात्मक होती है।]
अब, ΔSTR का क्षेत्रफल = `1/2 xx TR xx TS` ...[∵ त्रिभुज का क्षेत्रफल = `1/2` (आधार × ऊंचाई)]
= `1/2 xx 12 xx 5`
= 30 m2
अब, आयत PQRT का क्षेत्रफल = PQ × RQ ...[∵ आयत का क्षेत्रफल = लंबाई × चौड़ाई]
= 12 × 7
= 84 m2 ...[∵ PQ = TR = 12 m]
∴ समलंब का क्षेत्रफल = ΔSTR का क्षेत्रफल + आयत PQRT का क्षेत्रफल
= 30 + 84
= 114 m2
अतः, समलंब का क्षेत्रफल 114 m2 है।
APPEARS IN
RELATED QUESTIONS
एक पार्क चतुर्भुज ABCD के आकार का है, जिसमें ∠C = 90° है, AB = 9 मी, BC = 12 मी, CD = 5 मी और AD = 8 मी है। इस पार्क का क्षेत्रफल कितना है?
एक चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए, जिसमें AB = 3 सेमी, BC = 4 सेमी, CD = 4 सेमी, DA = 5 सेमी और AC = 5 सेमी हैं।
राधा ने एक रंगीन कागज़ से एक हवाईजहाज़ का चित्र बनाया, जैसा कि आकृति में दिखाया गया है। प्रयोग किए गए कागज़ का कुल क्षेत्रफल ज्ञात कीजिए।
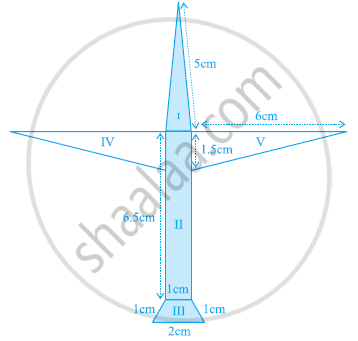
एक समचतर्भजाकार घास के खेत में 18 गायों के चरने के लिए घास है। यदि इस समचतुर्भुज की प्रत्येक भुजा 30 मी है और बड़ा विकर्ण 48 मी है, तो प्रत्येक गाय को चरने के लिए इस घास के खेत का कितना क्षेत्रफल प्राप्त होगा?
एक पतंग तीन भिन्न-भिन्न रंगों के कागज़ों से बनी है। इन्हें आकृति में I, II और III से दर्शाया गया है। पतंग का ऊपरी भाग 32 सेमी विकर्ण का एक वर्ग है और निचला भाग 6 सेमी, 6 सेमी और 8 सेमी भुजाओं का एक समद्विबाहु त्रिभुज है। ज्ञात कीजिए कि प्रत्येक रंग का कितना कागज़ प्रयुक्त किया गया है।
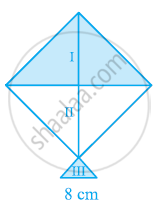
एक खेत समलंब के आकार का है जिसकी समांतर भुजाएँ 25 मी और 10 मी हैं। इसकी असमांतर भुजाएँ 14 मी और 13 मी हैं। इस खेत का क्षेत्रफल ज्ञात कीजिए।
एक त्रिभुज की भुजाएँ 11 cm, 12 cm और 13 cm की हैं। 12 cm लंबी भुजा के संगत शीर्षलंब की लंबाई 10.25 cm हैं।
एक खेत एक समांतर चतुर्भुज के आकार का है, जिसकी भुजाएँ 60 m और 40 m हैं तथा एक विकर्ण 80 m है। इस खेत का क्षेत्रफल ज्ञात कीजिए।
एक चतुर्भुज ABCD की भुजाएँ (एक क्रम में लेने पर) 6 cm, 8 cm, 12 cm और 14 cm हैं तथा प्रथम दो भुजाओं के बीच का कोण समकोण है। इसका क्षेत्रफल ज्ञात कीजिए।
एक मकान का निर्माण करने के लिए एक आयताकार भूखंड दिया गया, जिसकी लंबाई 40 m है तथा सामने की चौडाई 15 m है। नियमों के अनुसार, सामने और पीछे की ओर न्यूनतम 3 m चौड़ी जगह तथा प्रत्येक अन्य ओर पर न्यूनतम 2 m चौड़ी जगह छोड़नी आवश्यक है। वह अधिकतम क्षेत्र ज्ञात कीजिए जिसमें मकान का निर्माण किया जा सकता है।
