Advertisements
Chapters
![NCERT Exemplar solutions for Mathematics [Hindi] Class 9 chapter 12 - हीरोन का सूत्र NCERT Exemplar solutions for Mathematics [Hindi] Class 9 chapter 12 - हीरोन का सूत्र - Shaalaa.com](/images/mathematics-hindi-class-9_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 12: हीरोन का सूत्र
Below listed, you can find solutions for Chapter 12 of CBSE NCERT Exemplar for Mathematics [Hindi] Class 9.
NCERT Exemplar solutions for Mathematics [Hindi] Class 9 12 हीरोन का सूत्र प्रश्नावली 12.1 [Page 115]
निम्नलिखित में से प्रत्येक में सही उत्तर लिखिए -
एक समद्विबाहु समकोण त्रिभुज का क्षेत्रफल 8 cm2 है। इसके कर्ण की लंबाई है।
`sqrt(32)` cm
`sqrt(16)` cm
`sqrt(48)` cm
`sqrt(24)` cm
एक समबाहु त्रिभुज का परिमाप 60 m है। इसका क्षेत्रफल है
`10sqrt(3)` m2
`15sqrt(3)` m2
`20sqrt(3)` m2
`100sqrt(3)` m2
एक त्रिभुज की भुजाएँ 56 cm, 60 cm और 52 cm लंबाईयों की हैं। तब, त्रिभुज का क्षेत्रफल है
1322 cm2
1311 cm2
1344 cm2
1392 cm2
`2sqrt(3)` cm भुजा वाले समबाहु त्रिभुज का क्षेत्रफल है
5.196 cm2
0.866 cm2
3.496 cm2
1.732 cm2
क्षेत्रफल `9sqrt(3)` cm2 वाले एक समबाहु त्रिभुज की प्रत्येक भुजा की लंबाई है
8 cm
36 cm
4 cm
6 cm
यदि एक समबाहु त्रिभुज का क्षेत्रफल `16sqrt(3)` cm2 है, तो इस त्रिभुज का परिमाप है
48 cm
24 cm
12 cm
36 cm
एक त्रिभुज की भुजाएँ 35 cm, 54 cm और 61 cm की हैं। इसके सबसे लंबे शीर्षलंब की लंबाई है
`16sqrt(5)` cm
`10sqrt(5)` cm
`24sqrt(5)` cm
28 cm
आधार 2 cm और बराबर भुजाओं में से एक भुजा 4 cm वाले समद्विबाहु त्रिभुज का क्षेत्रफल है
`sqrt(15)` cm2
`sqrt(15/2)` cm2
`2sqrt(15)` cm2
`4sqrt(15)` cm2
एक त्रिभुजाकार बोर्ड के किनारे 6 cm, 8 cm और 10 cm लंबाईयों के हैं। इस पर 9 पैसे प्रति cm2 की दर से पेंट कराने का व्यय है
2.00 रु
2.16 रु
2.48 रु
3.00 रु
NCERT Exemplar solutions for Mathematics [Hindi] Class 9 12 हीरोन का सूत्र प्रश्नावली 12.2 [Page 116]
सत्य या असत्य लिखिए तथा अपने उत्तर का औचित्य दीजिए -
आधार 4 cm और ऊँचाई 6 cm वाले त्रिभुज का क्षेत्रफल 24 cm2 है।
सत्य
असत्य
एक त्रिभुज ABC का क्षेत्रफल 8 cm2 है, जिसमें AB = AC = 4 cm है तथा ∠A = 90° है।
सत्य
असत्य
एक समद्विबाहु त्रिभुज का क्षेत्रफल `5/4 sqrt(11)` cm2 होगा, यदि उसका परिमाप 11 cm है और आधार 5 cm है।
सत्य
असत्य
एक समबाहु त्रिभुज का क्षेत्रफल `20sqrt(3)` cm2 है, जिसकी प्रत्येक भुजा 8 cm है।
सत्य
असत्य
यदि एक समचतुर्भुज की एक भुजा 10 cm और एक विकर्ण 16 cm है, तो उस समचतुर्भुज का क्षेत्रफल 96 cm2 है।
सत्य
असत्य
एक समांतर चतुर्भुज का आधार और संगत शीर्षलंब क्रमश : 10 cm और 3.5 cm हैं। उस समांतर चतुर्भुज का क्षेत्रफल 30 cm2 है।
सत्य
असत्य
भुजा a वाले एक समषड्भुज का क्षेत्रफल भुजा a वाले पाँच समबाहु त्रिभुजों के क्षेत्रफलों के योग के बराबर होता है।
सत्य
असत्य
एक त्रिभुजाकार मैदान जिसकी भुजाएँ 51 m, 37 m और 20 m हैं को 3 रु. प्रति m2 की दर से समतल कराने का व्यय 918 रु है।
सत्य
असत्य
एक त्रिभुज की भुजाएँ 11 cm, 12 cm और 13 cm की हैं। 12 cm लंबी भुजा के संगत शीर्षलंब की लंबाई 10.25 cm हैं।
सत्य
असत्य
NCERT Exemplar solutions for Mathematics [Hindi] Class 9 12 हीरोन का सूत्र प्रश्नावली 12.3 [Pages 118 - 119]
भुजाओं 50 m, 65 m और 65 m वाले त्रिभुजाकार खेत में 7 रु. प्रति m2 की दर से घास लगवाने का व्यय ज्ञात कीजिए।
एक फ्लाईओवर की त्रिभुजाकार पार्श्व दीवारों को विज्ञापनों के लिए प्रयोग किया जाता है। दीवारों की भुजाएँ 13 m, 14 m और 15m हैं। विज्ञापनों से एक वर्ष में 2000 रु प्रति m2 की दर से आय होती है। एक कंपनी इनमें से एक दीवार को 6 महीने के लिए किराए पर लेती है। उस कंपनी ने कितना किराया दिया होगा?
एक समबाहु त्रिभुज के अभ्यंतर में स्थित किसी बिंदु से तीनों भुजाओं पर लंब डाले जाते हैं। इन लंबों की लंबाई 14 cm, 10 cm और 6 cm हैं। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
एक समद्विबाहु त्रिभुज का परिमाप 32 cm है। एक बराबर भुजा और आधार का अनुपात 3 : 2 है। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
आकृति में दिए हुए समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए। साथ ही, शीर्ष A से भुजा DC पर शीर्षलंब की लंबाई ज्ञात कीजिए।
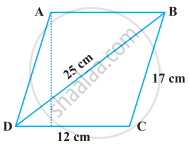
एक खेत एक समांतर चतुर्भुज के आकार का है, जिसकी भुजाएँ 60 m और 40 m हैं तथा एक विकर्ण 80 m है। इस खेत का क्षेत्रफल ज्ञात कीजिए।
एक त्रिभुजाकार खेत का परिमाप 420 m है तथा इसकी भुजाओं का अनुपात 6 : 7 : 8 है। इस खेत का क्षेत्रफल ज्ञात कीजिए।
एक चतुर्भुज ABCD की भुजाएँ (एक क्रम में लेने पर) 6 cm, 8 cm, 12 cm और 14 cm हैं तथा प्रथम दो भुजाओं के बीच का कोण समकोण है। इसका क्षेत्रफल ज्ञात कीजिए।
एक समचतुर्भुज के आकार की शीट (चादर), जिसका परिमाप 40 cm और एक विकर्ण 12 cm है, को दोनों ओर से 5 रु प्रति m2 की दर से पेंट किया जाता है। पेंट करवाने की लागत ज्ञात कीजिए।
निम्नलिखित आकृति में दी हुई ऊँचाई PQ वाले समलंब PORS का क्षेत्रफल ज्ञात कीजिए।
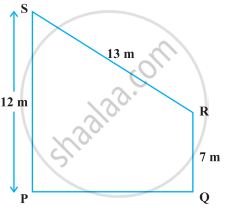
NCERT Exemplar solutions for Mathematics [Hindi] Class 9 12 हीरोन का सूत्र प्रश्नावली 12.4 [Pages 120 - 122]
निम्नलिखित आकृति में दी हुई पतंग को बनाने के लिए प्रत्येक शेड (रंग) के कितने कागज की आवश्यकता होगी, यदि ABCD विकर्ण 44 cm वाला एक वर्ग है।
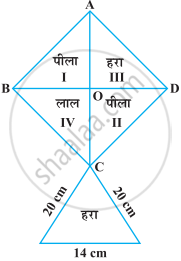
एक त्रिभुज का परिमाप 50 cm है। त्रिभुज की एक भुजा छोटी भुजा से 4 cm लंबी है तथा तीसरी भुजा छोटी भुजा के दुगुने से 6 cm कम है। त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
एक समलंब का क्षेत्रफल 475 cm2 है तथा ऊँचाई 19 cm है। इसकी समांतर भुजाओं की लंबाइयाँ ज्ञात कीजिए, यदि एक समांतर भुजा दूसरी समांतर भुजा से 4 cm अधिक है।
एक मकान का निर्माण करने के लिए एक आयताकार भूखंड दिया गया, जिसकी लंबाई 40 m है तथा सामने की चौडाई 15 m है। नियमों के अनुसार, सामने और पीछे की ओर न्यूनतम 3 m चौड़ी जगह तथा प्रत्येक अन्य ओर पर न्यूनतम 2 m चौड़ी जगह छोड़नी आवश्यक है। वह अधिकतम क्षेत्र ज्ञात कीजिए जिसमें मकान का निर्माण किया जा सकता है।
एक खेत समलंब के आकार का है, जिसकी समांतर भुजाएँ 90 m और 30 m की हैं। ये दोनों भुजाएँ तीसरी भुजा से समकोण पर मिलती हैं। चौथी भुजा की लंबाई 100 m की है। यदि 1 m2 खेत की जुताई की लागत 4 रु है, तो खेत की जुताई में लगने वाली कुल लागत ज्ञात कीजिए।
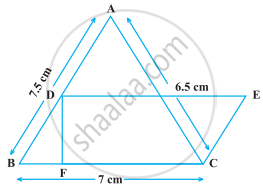
निम्नलिखित आकृति में, ∆ABC की भुजाओं में AB = 7.5 cm, AC = 6.5 cm और BC = 7 cm है। आधार BC पर एक समांतर चतुर्भुज DBCE की रचना की जाती है, जो क्षेत्रफल में ∆ABC के बराबर है। इस समांतर चतुर्भुज की ऊँचाई DF ज्ञात कीजिए।
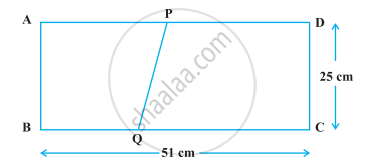
एक आयत ABCD की विमाएँ 51 cm × 25 cm हैं। इस आयत में से एक समलंब PQCD काटा जाता है, जिसकी समांतर भुजाएँ QC और PD हैं और ये 9 : 8 के अनुपात में हैं, जैसा कि निम्नलिखित आकृति में दर्शाया गया है। यदि समलंब PQCD का क्षेत्रफल आयत के क्षेत्रफल का `5/6` भाग है, तो QC और PD की लंबाइयाँ ज्ञात कीजिए।
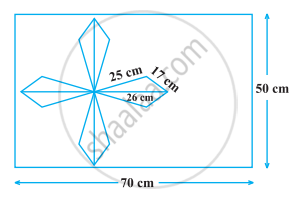
50 cm × 70 cm विमाओं वाली एक आयताकार टाइल पर, निम्नलिखित आकृति में दर्शाए अनुसार एक डिज़ाइन बनाया जाता है। इस डिज़ाइन में 8 त्रिभुज हैं, जिनमें से प्रत्येक की भुजा 26 cm, 17 cm और 25 cm की हैं। डिज़ाइन का पूर्ण क्षेत्रफल ज्ञात कीजिए तथा टाइल के शेष भाग का क्षेत्रफल भी ज्ञात कीजिए।
Solutions for 12: हीरोन का सूत्र
![NCERT Exemplar solutions for Mathematics [Hindi] Class 9 chapter 12 - हीरोन का सूत्र NCERT Exemplar solutions for Mathematics [Hindi] Class 9 chapter 12 - हीरोन का सूत्र - Shaalaa.com](/images/mathematics-hindi-class-9_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
NCERT Exemplar solutions for Mathematics [Hindi] Class 9 chapter 12 - हीरोन का सूत्र
Shaalaa.com has the CBSE Mathematics Mathematics [Hindi] Class 9 CBSE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. NCERT Exemplar solutions for Mathematics Mathematics [Hindi] Class 9 CBSE 12 (हीरोन का सूत्र) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. NCERT Exemplar textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [Hindi] Class 9 chapter 12 हीरोन का सूत्र are त्रिभुज का क्षेत्रफल, त्रिभुज का क्षेत्रफल - हीरोन के सूत्र द्वारा, चतुर्भुजों के क्षेत्रफल ज्ञात करने में हीरोन के सूत्र का अनुप्रयोग.
Using NCERT Exemplar Mathematics [Hindi] Class 9 solutions हीरोन का सूत्र exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in NCERT Exemplar Solutions are essential questions that can be asked in the final exam. Maximum CBSE Mathematics [Hindi] Class 9 students prefer NCERT Exemplar Textbook Solutions to score more in exams.
Get the free view of Chapter 12, हीरोन का सूत्र Mathematics [Hindi] Class 9 additional questions for Mathematics Mathematics [Hindi] Class 9 CBSE, and you can use Shaalaa.com to keep it handy for your exam preparation.
