Advertisements
Advertisements
Question
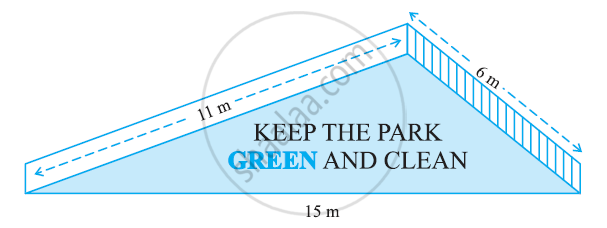
किसी पार्क में एक फिसल पट्टी (Slide) बनी हुई है। इसकी पार्श्वीय दीवारों (Side Walls) में से एक दीवार पर किसी रंग से पेंट किया गया है और उस पर ‘‘पार्क को हरा-भरा और साफ़ रखिए” लिखा हुआ है। (देखिए आकृति)। यदि इस दीवार की विमाएँ 15 m, 11 m और 6 m हैं, तो रंग से पेंट हुए भाग का क्षेत्रफल ज्ञात कीजिए।
Solution
यह देखा जा सकता है कि रंग से रंगा जाने वाला क्षेत्र एक त्रिभुज है, जिसकी भुजाएँ 11 m, 6 m और 15 m हैं।
ऐसे त्रिभुज का परिमाप = (11 + 6 + 15) m
2 s = 32 m
s =`32/2 m`
s = 16 m
हीरोन के सूत्र से,
त्रिभुज का क्षेत्रफल = `sqrt(s(s-a)(s-b)(s-c))`
= `[sqrt(16(16-11)(16-6)(16-15))]m^2`
= `(sqrt(16xx5xx10xx1))m^2`
= `20sqrt2m^2`
इसलिए, रंग से पेंट हुए भाग का क्षेत्रफल `20sqrt2m^2` है।
APPEARS IN
RELATED QUESTIONS
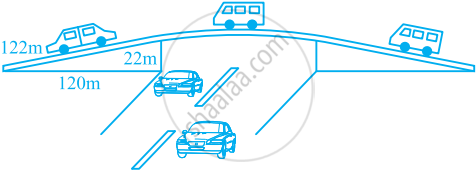
किसी फ्लाईओवर (Flyover) की त्रिभुजाकार दीवार को विज्ञापनों के लिए प्रयोग किया जाता है। दीवार की भुजाओं की लंबाइयाँ 122 m, 22 m और 120 m हैं (देखिए आकृति)। इस विज्ञापन से प्रति वर्ष ₹ 5000 प्रति m2 की प्राप्ति होती है। एक कंपनी ने एक दीवार को विज्ञापन देने के लिए 3 महीने के लिए किराए पर लिया। उसने कुल कितना किराया दिया?
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी दो भुजाएँ 18 cm और 10 cm हैं तथा उसका परिमाप 42 cm है।
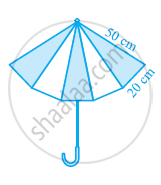
दो विभिन्न रंगों के कपड़ों के 10 त्रिभुजाकार टुकड़ों की सिलाई करके एक छाता बनाया गया है (देखिए आकृति) प्रत्येक टुकड़े के माप 20 सेमी, 50 सेमी और 50 सेमी हैं। छाते में प्रत्येक रंग का कितना कपड़ा लगा है?
यदि एक समबाहु त्रिभुज का क्षेत्रफल `16sqrt(3)` cm2 है, तो इस त्रिभुज का परिमाप है
यदि एक समचतुर्भुज की एक भुजा 10 cm और एक विकर्ण 16 cm है, तो उस समचतुर्भुज का क्षेत्रफल 96 cm2 है।
एक समांतर चतुर्भुज का आधार और संगत शीर्षलंब क्रमश : 10 cm और 3.5 cm हैं। उस समांतर चतुर्भुज का क्षेत्रफल 30 cm2 है।
भुजा a वाले एक समषड्भुज का क्षेत्रफल भुजा a वाले पाँच समबाहु त्रिभुजों के क्षेत्रफलों के योग के बराबर होता है।
एक समचतुर्भुज के आकार की शीट (चादर), जिसका परिमाप 40 cm और एक विकर्ण 12 cm है, को दोनों ओर से 5 रु प्रति m2 की दर से पेंट किया जाता है। पेंट करवाने की लागत ज्ञात कीजिए।
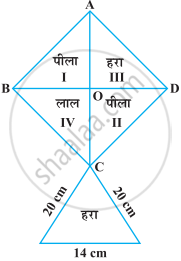
निम्नलिखित आकृति में दी हुई पतंग को बनाने के लिए प्रत्येक शेड (रंग) के कितने कागज की आवश्यकता होगी, यदि ABCD विकर्ण 44 cm वाला एक वर्ग है।
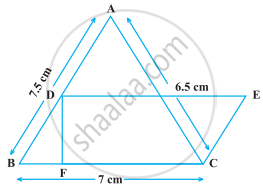
निम्नलिखित आकृति में, ∆ABC की भुजाओं में AB = 7.5 cm, AC = 6.5 cm और BC = 7 cm है। आधार BC पर एक समांतर चतुर्भुज DBCE की रचना की जाती है, जो क्षेत्रफल में ∆ABC के बराबर है। इस समांतर चतुर्भुज की ऊँचाई DF ज्ञात कीजिए।