Advertisements
Advertisements
प्रश्न
एक यातायात संकेत बोर्ड पर 'आगे स्कूल है’ लिखा है और यह भुजा ‘a‘ वाले एक समबाहु त्रिभुज के आकार का है। हीरोन के सूत्र का प्रयोग करके इस बोर्ड का क्षेत्रफल ज्ञात कीजिए। यदि संकेत बोर्ड का परिमाप 180 cm है, तो इसका क्षेत्रफल क्या होगा?
उत्तर
यातायात संकेत बोर्ड की भुजा = a
यातायात संकेत बोर्ड का परिमाप = 3 × a
2s = 3a ⇒ s = `3/2 a`
हीरोन के सूत्र से,
त्रिभुज का क्षेत्रफल = `sqrt(s(s-a)(s-b)(s-c))`
दिए गए त्रिभुज का क्षेत्रफल = `sqrt(3/2 a(3/2a-a)(3/2a-a)(3/2a-a))`
= `sqrt((3/2a)(a/2)(a/2)(a/2))`
= `sqrt3/4a^2` ...(1)
यातायात संकेत बोर्ड का परिमाप = 180 cm
यातायात संकेत बोर्ड की भुजा (a) = `(180/3) cm` = 60 cm
समीकरण (1) का उपयोग करते हुए, यातायात संकेत बोर्ड का क्षेत्रफल
= `sqrt3/4(60cm)^2`
= `(3600/4sqrt3)cm^2` = `900sqrt3 cm^2`
APPEARS IN
संबंधित प्रश्न
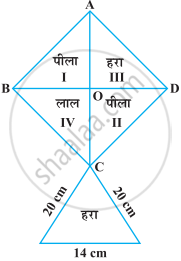
किसी फ्लाईओवर (Flyover) की त्रिभुजाकार दीवार को विज्ञापनों के लिए प्रयोग किया जाता है। दीवार की भुजाओं की लंबाइयाँ 122 m, 22 m और 120 m हैं (देखिए आकृति)। इस विज्ञापन से प्रति वर्ष ₹ 5000 प्रति m2 की प्राप्ति होती है। एक कंपनी ने एक दीवार को विज्ञापन देने के लिए 3 महीने के लिए किराए पर लिया। उसने कुल कितना किराया दिया?
एक त्रिभुज की भुजाओं का अनुपात 12 : 17 : 25 है और उसका परिमाप 540 cm है। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
क्षेत्रफल `9sqrt(3)` cm2 वाले एक समबाहु त्रिभुज की प्रत्येक भुजा की लंबाई है
यदि एक समबाहु त्रिभुज का क्षेत्रफल `16sqrt(3)` cm2 है, तो इस त्रिभुज का परिमाप है
एक त्रिभुज की भुजाएँ 35 cm, 54 cm और 61 cm की हैं। इसके सबसे लंबे शीर्षलंब की लंबाई है
यदि एक समचतुर्भुज की एक भुजा 10 cm और एक विकर्ण 16 cm है, तो उस समचतुर्भुज का क्षेत्रफल 96 cm2 है।
भुजाओं 50 m, 65 m और 65 m वाले त्रिभुजाकार खेत में 7 रु. प्रति m2 की दर से घास लगवाने का व्यय ज्ञात कीजिए।
एक समद्विबाहु त्रिभुज का परिमाप 32 cm है। एक बराबर भुजा और आधार का अनुपात 3 : 2 है। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
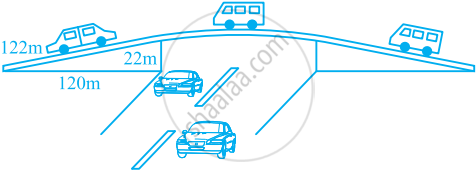
आकृति में दिए हुए समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए। साथ ही, शीर्ष A से भुजा DC पर शीर्षलंब की लंबाई ज्ञात कीजिए।
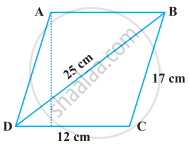
निम्नलिखित आकृति में दी हुई पतंग को बनाने के लिए प्रत्येक शेड (रंग) के कितने कागज की आवश्यकता होगी, यदि ABCD विकर्ण 44 cm वाला एक वर्ग है।