Advertisements
Advertisements
Question
Factorize a3 x3 - 3a2bx2 + 3ab2 x - b3
Solution
= (ax)3 - 3(ax)2 × b + 3(ax)b2 - b3
= (ax - b)3 [∵ a2 - 3a2b + 3ab2 - b3 = (a - b)3 ]
= (ax - b)(ax - b)(ax - b)
∴ a3 x3 - 3a2bx2 + 3ab2 x - b3 = (ax - b)(ax - b)(ax - b)
APPEARS IN
RELATED QUESTIONS
Factorize x4 + x2 y2 + y4
`(x/2 + y + z/3)^3 + (x/2 + (2y)/3 + z)^3 + (-(5x)/6 - y/3 - (4z)/3)^3`
If a + b + c = 9 and ab + bc + ca = 40, find a2 + b2 +c2.
If (x + y)3 − (x − y)3 − 6y(x2 − y2) = ky2, then k =
Evaluate: (c + 5)(c - 3)
Divide: n2 - 2n + 1 by n - 1
Divide: x3 − 6x2 + 11x − 6 by x2 − 4x + 3
Write the coefficient of x2 and x in the following polynomials
`sqrt(3)x^2 + sqrt(2)x + 0.5`
The constant term of the expression 2y – 6 is _________
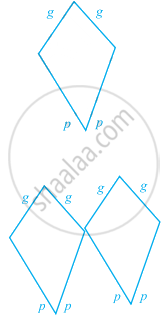
In the given figure, the length of a green side is given by g and that of the red side is given by p.
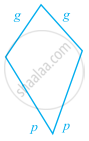
Write an expression for the following pattern. Also write an expression if 100 such shapes are joined together.