Advertisements
Advertisements
Question
Figure represents a crystal unit of cesium chloride, CsCl. The cesium atoms, represented by open circles are situated at the corners of a cube of side 0.40 nm, whereas a Cl atom is situated at the centre of the cube.
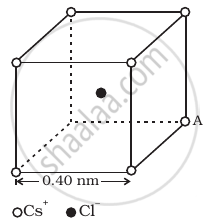
The Cs atoms are deficient in one electron while the Cl atom carries an excess electron.
- What is the net electric field on the Cl atom due to eight Cs atoms?
- Suppose that the Cs atom at the corner A is missing. What is the net force now on the Cl atom due to seven remaining Cs atoms?
Solution
- Zero, from symmetry.
- Removing a +ve Cs ion is equivalent to adding singly charged –ve Cs ion at that location.
Net force then is F = `e^2/(4pi ε_0 r^2)`
Where r = distance between the Cl ion and a Cs ion.
= `sqrt((0.20)^2 + (0.20)^2 + (0.20)^2) xx 10^-9` m
= `sqrt(3(0.20)^2) xx 10^-9` m
= 0.346 × 10–9 m
Hence, F = `((8.99 xx 10^9)(1.6 xx 10^-19)^2)/(0.346 xx 10^-9)^2` = 192 × 10–11
= 1.92 × 10–9 N, directed from A to Cl–
APPEARS IN
RELATED QUESTIONS
Explain the meaning of the statement ‘electric charge of a body is quantised’.
Does the charge given to a metallic sphere depend on whether it is hollow or solid? Give reason for your answer.
When a charged comb is brought near a small piece of paper, it attracts the piece. Does the paper become charged when the comb is brought near it?
+2 C and +6 C two charges are repelling each other with a force of 12 N. If each charge is given -2 C of charge, then the value of the force will be ______
Conservation of charges in tribo electric charging _________.
Charge is quantized means ______.
The number of lines of force that radiate outwards from one coulomb of charge is:-
Eight dipoles of charge of magnitude ± e are placed inside a cube. The total electric flux coming out of the cube will be:-
The dimensions of an atom are of the order of an Angstrom. Thus there must be large electric fields between the protons and electrons. Why, then is the electrostatic field inside a conductor zero?
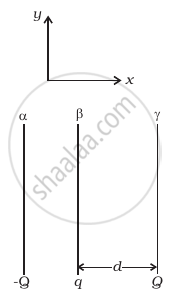
Two fixed, identical conducting plates (α and β), each of surface area S are charged to –Q and q, respectively, where Q > q > 0. A third identical plate (γ), free to move is located on the other side of the plate with charge q at a distance d (Figure). The third plate is released and collides with the plate β. Assume the collision is elastic and the time of collision is sufficient to redistribute charge amongst β and γ.
- Find the electric field acting on the plate γ before collision.
- Find the charges on β and γ after the collision.
- Find the velocity of the plate γ after the collision and at a distance d from the plate β.