Advertisements
Advertisements
Question
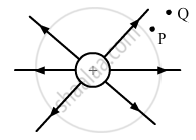
Figure shows the field lines due to a positive point charge. Give the sign of potential energy difference of a small negative charge between the points Q and P.
Solution
The electric potential at a point distant r due to the field created by a positive charge Q is given by
\[v = \frac{1}{4\pi \epsilon_0}\frac{q}{r}\]
Since rQ > rP, we have:
VQ < VP
∴ The potential energy difference VP − VQ is positive between Q and P.
APPEARS IN
RELATED QUESTIONS
A cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge array at the centre of the cube.
If one of the two electrons of a H2 molecule is removed, we get a hydrogen molecular ion `"H"_2^+`. In the ground state of an `"H"_2^+`, the two protons are separated by roughly 1.5 Å, and the electron is roughly 1 Å from each proton. Determine the potential energy of the system. Specify your choice of zero potential energy.
Four point charges Q, q, Q and q are placed at the corners of a square of side 'a' as shown in the figure.
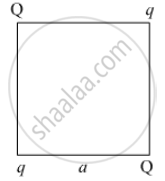
Find the
1) resultant electric force on a charge Q, and
2) potential energy of this system.
A point charge Q is placed at point 'O' as shown in the figure. Is the potential at point A, i.e. VA, greater, smaller or equal to potential, VB, at point B, when Q is (i) positive, and (ii) negative charge?
A point charge Q is placed at point O as shown in the figure. The potential difference VA – VB positive. Is the charge Q negative or positive?

If a charge q0 is there in an electric field caused by several point charges qi. The potential energy of q0 is given by ________.
Consider a uniform electric field in the z-direction. The potential is a constant ______.
In the circuit shown in figure initially, key K1 is closed and key K2 is open. Then K1 is opened and K2 is closed (order is important). [Take Q1′ and Q2′ as charges on C1 and C2 and V1 and V2 as voltage respectively.]

Then
- charge on C1 gets redistributed such that V1 = V2
- charge on C1 gets redistributed such that Q1′ = Q2′
- charge on C1 gets redistributed such that C1V1 + C2V2 = C1E
- charge on C1 gets redistributed such that Q1′ + Q2′ = Q
- In a quark model of elementary particles, a neutron is made of one up quarks [charge (2/3) e] and two down quarks [charges –(1/3) e]. Assume that they have a triangle configuration with side length of the order of 10–15 m. Calculate electrostatic potential energy of neutron and compare it with its mass 939 MeV.
- Repeat above exercise for a proton which is made of two up and one down quark.
Charges (+q) and (–q) are placed at points A and B respectively which are a distance 2L apart. C is the midpoint between A and B. What is the work done in moving a charge +Q along the semicircle CRD?