Advertisements
Advertisements
Question
Find a vector of magnitude 11 in the direction opposite to that of `vec"PQ"` where P and Q are the points (1, 3, 2) and (–1, 0, 8), respectively.
Solution
The vector with initial point P (1, 3, 2) and terminal point Q (–1, 0, 8) is given by
`vec"PQ" = (-1 - 1) hat"i" + (0 - 3) hat"j" + (8 - 2) hat"k"`
= `-2hat"i" - 3hat"j" + 6hat"k"`
Thus `vec"OP" = - vec"PQ" = 2hat"i" + 3hat"j" - 6hat"k"`
⇒ `|vec"OP"| = sqrt(2^2 + 3^2 + (-6)^2)`
= `sqrt(4 + 9 + 36)`
= `sqrt(49)`
= 7
Therefore, unit vector in the direction of `vec"OP"` is given by
`hat"OP" = vec"OP"/|vec"OP"|`
= `(2hat"i" + 3hat"j" - 6hat"k")/7`
Hence, the required vector of magnitude 11 in direction of `vec"OP"` is 11
`hat"OP" = 11((2hat"i" + 3hat"j" - 6hat"k")/7)`
= `22/7hat"i" + 33/7hat"j" - 66/7 hat"k"`.
APPEARS IN
RELATED QUESTIONS
If a vector makes angles α, β, γ with OX, OY and OZ respectively, then write the value of sin2 α + sin2 β + sin2 γ.
The vector equation of the plane passing through \[\vec{a} , \vec{b} , \vec{c} ,\text{ is }\vec{r} = \alpha \vec{a} + \beta \vec{b} + \gamma \vec{c} ,\] provided that
If three points A, B and C have position vectors \[\hat{i} + x \hat{j} + 3 \hat{k} , 3 \hat{i} + 4 \hat{j} + 7 \hat{k}\text{ and }y \hat{i} - 2 \hat{j} - 5 \hat{k}\] respectively are collinear, then (x, y) =
ABCD is a parallelogram with AC and BD as diagonals.
Then, \[\overrightarrow{AC} - \overrightarrow{BD} =\]
If` vec"a" = 2hat"i" + 3hat"j" + + hat"k", vec"b" = hat"i" - 2hat"j" + hat"k" "and" vec"c" = -3hat"i" + hat"j" + 2hat"k", "find" [vec"a" vec"b" vec"c"]`
In the triangle PQR, `bar"PQ" = bar"2a", bar"QR" = bar"2b"`. The midpoint of PR is M. Find the following vectors in terms of `bar"a"` and `bar"b"`:
(i) `bar"PR"` (ii) `bar"PM"` (iii) `bar"QM"`.
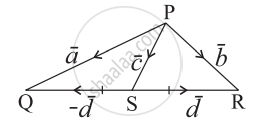
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
If two sides of a triangle are `hat"i" + 2hat"j" and hat"i" + hat"k"`, find the length of the third side.
Find the lengths of the sides of the triangle and also determine the type of a triangle:
A(2, -1, 0), B(4, 1, 1), C(4, -5, 4)
If ABC is a triangle whose orthocentre is P and the circumcentre is Q, prove that `bar"PA" + bar"PB" + bar"PC" = 2bar"PQ".`
Express the vector `bar"a" = 5hat"i" - 2hat"j" + 5hat"k"` as a sum of two vectors such that one is parallel to the vector `bar"b" = 3hat"i" + hat"k"` and other is perpendicular to `bar"b"`.
Find the angle between the lines whose direction cosines are given by the equations 6mn - 2nl + 5lm = 0, 3l + m + 5n = 0.
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a" xx (bar"b".bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a" xx(bar"b" xx bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`(bar"a".bar"b") xx (bar"c".bar"d")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`|bar"a"|(bar"b".bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a".(bar"b" + bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a". bar"b" + bar"c"`
The vector eqliation of line 2x - 2 = 3y + 1 = 6z - 2 is
The points A(- a, -b), B (0, 0), C(a, b) and D(a2 , ab) are ______.
If `vec"a"` is any non-zero vector, then `(vec"a" .hat"i")hat"i" + (vec"a".hat"j")hat"j" + (vec"a".hat"k")hat"k"` equals ______.
Classify the following as scalar and vector quantity.
Velocity
The unit vector perpendicular to the vectors `6hati + 2hatj + 3hatk` and `3hati - 6hatj - 2hatk` is
Find `|vecx|` if `(vecx - veca).(vecx + veca)` = 12, where `veca` is a unit vector.
If points P(4, 5, x), Q(3, y, 4) and R(5, 8, 0) are collinear, then the value of x + y is ______.
Check whether the vectors `2hati + 2hatj + 3hat k, -3hati + 3hatj + 2hat k` and `3hati + 4hatk` form a triangle or not.
In the triangle PQR, `bb(bar(PQ) = 2 bara)` and `bb(bar(QR) = 2 barb)`. The mid-point of PR is M. Find the following vectors in terms of `bb(bara and barb)`.
- `bar(PR)`
- `bar(PM)`
- `bar(QM)`
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
In the triangle PQR, `bar(PQ)` = 2`bara` and `bar(QR)` = 2`barb`. The midpoint of PR is M. Find the following vectors in terms of `bara` and `barb`.
(i) `bar(PR)` (ii) `bar(PM)` (iii) `bar(QM)`
