Advertisements
Advertisements
Question
Find all zeros of the polynomial 3x3 + 10x2 − 9x − 4 if one of its zero is 1.
Solution
Given: 3x3 + 10x2 - 9x - 5
Since 1 is a zero of the given polynomial. So, (x - 1) will be a factor of the given polynomial.
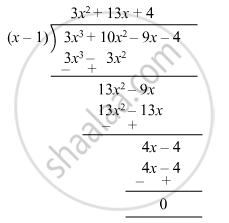
So, 3x3 + 10x2 - 9x - 4 = (x - 1)(3x2 + 13x + 4)
By splitting the middle term in (3x2 + 13x + 4) we factorised (3x2 + 13x + 4) as (3x + 1)(x + 4).
So, the zeroes are given by x = -4, `(-1)/3`
Thus, all the zeroes are x = -4, `(-1)/3,1`
APPEARS IN
RELATED QUESTIONS
Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following
p(x) = x4 – 5x + 6, g(x) = 2 – x2
Obtain all other zeroes of 3x4 + 6x3 – 2x2 – 10x – 5, if two of its zeroes are `sqrt(5/3)` and - `sqrt(5/3)`
Apply division algorithm to find the quotient q(x) and remainder r(x) on dividing f(x) by g(x) in the following f(x) = 4x3 + 8x2 + 8x + 7, g(x) = 2x2 − x + 1
Find all zeros of the polynomial f(x) = 2x4 − 2x3 − 7x2 + 3x + 6, if its two zeros are `-sqrt(3/2)` and `sqrt(3/2)`
Find all zeros of the polynomial 2x4 + 7x3 − 19x2 − 14x + 30, if two of its zeros are `sqrt2` and `-sqrt2`.
Find all the zeros of the polynomial x3 + 3x2 − 2x − 6, if two of its zeros are `-sqrt2` and `sqrt2`
It is given that –1 is one of the zeroes of the polynomial `x^3 + 2x^2 – 11x – 12`. Find all the zeroes of the given polynomial.
The area of a rectangle is x2 + 7x + 12. If its breadth is (x + 3), then find its length
The sum of (x + 5) observations is (x3 + 125). Find the mean of the observations
Which one of the following statements is correct?
