Advertisements
Advertisements
Question
Find the mass of lamina bounded by the curves ๐ = ๐๐ − ๐๐ and ๐ = ๐๐ if the density of the lamina at any point is given by `24/25 xy`
Solution
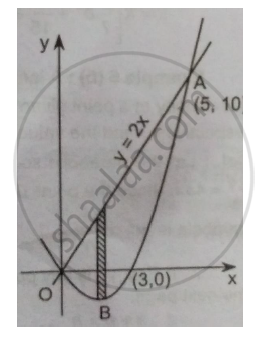
The curve `y=x^2-3x` i.e `y+9/4=(x-3/2)^2`parabola intersecting the x-axis in x = 0 and x = 3. The line y = 2x intersects this parabola at x2 – 3x = 2x i.e. x2 – 5x = 0 i.e. at x = 0, x = 5. Therefore, points of intersection are (0,0) and (5,10). The surface density is ρ = (24/25)xy.
Taking the elementary strip parallel to the y-axis, on the strip y varies from ๐ฆ = ๐ฅ2 − 3๐ฅ to ๐ฆ = 2๐ฅ and then x varies from x = 0 to x = 5.
∴ Mass of lamina = `int_0^5 int_(x^2-3x )^(2x) xydxdy`
=`24/25 int_0^5 x[y^2/2]_(x^2-3x)^(2x) 24/25 xydxdy`
`=24/50int_0^5 4x^3-x(x^4-6x^3+9x^2) dx`
=`24/50int_0^5-5x^3+6x^4-x^5 dx`
=`24/50[-x^6/b+ (6x^5)/5-(5x^4)/4]_0^5`
=`24/50. 5^4 [-25/6+6-5/4]`
=`24/50. 5^4. 7/12`
∴ Mass of lamina = 175.
APPEARS IN
RELATED QUESTIONS
Evaluate `(d^4y)/(dx^4)+2(d^2y)/(dx^2)+y=0`
Evaluate `(2x+1)^2(d^2y)/(dx^2)-2(2x+1)(dy)/(dx)-12y=6x`
A resistance of 100 ohms and inductance of 0.5 henries are connected in series With a battery of 20 volts. Find the current at any instant if the relation between L,R,E is L `(di)/(dt)+Ri=E.`
Solve `(D^3+1)^2y=0`
Solve `(D^3+D^2+D+1)y=sin^2x`
Solve the ODE `(D-1)^2 (D^2+1)^2y=0`
Evaluate `int_0^1 int_0^(x2) y/(ex) dy dx`
Evaluate `int_0^1( x^a-1)/log x dx`
Solve `(1+x)^2(d^2y)/(dx^2)+(1+x)(dy)/(dx)+y=4cos(log(1+x))`
Find the length of cycloid from one cusp to the next , where `x=a(θ + sinθ) , y=a(1-cosθ)`
Solve `(D^2-3D+2) y= 2 e^x sin(x/2)`
Using D.U.I.S prove that `int_0^∞ e^-(x^+a^2/x^2) dx=sqrtpi/2 e^(-2a), a> 0`
Solve `(D^2+2)y=e^xcosx+x^2e^(3x)`
Evaluate `int_0^1int_0^( 1-x)1int_0^( 1-x-y) 1/(x+y+z+1)^3 dx dy dz`
Find the mass of the lemniscate ๐๐=๐๐๐๐๐ ๐๐ฝ if the density at any point is Proportional to the square of the distance from the pole .
Solve` x^2 (d^3y)/dx^3+3x (d^2y)/dx^2+dy/dx+y/x=4log x`
Solve `(D^2-7D-6)y=(1+x^2)e^(2x)`
Apply Rungee Kutta method of fourth order to find an approximate Value of y when x=0.4 given that `dy/dx=(y-x)/(y+x),y=1` ๐=๐ ๐๐๐๐ ๐=๐ Taking h=0.2.
Solve by variation of parameters` ((d^2y)/dx^2+1)y=1/(1+sin x)`
Compute the value of `int _0.2^1.4 (sin x - In x+e^x) ` Trapezoidal Rule (ii) Simpson’s (1/3)rd rule (iii) Simpson’s (3/8)th rule by dividing Into six subintervals.
Evaluate `int_0^(a/sqrt2) int_y^(sqrt(a2-y^2)) log (x^2+y^2) "dxdy by changing to polar Coordinates".`
Evaluate `int int int x^2` `yzdzdydz`over the volume bounded by planes x=0, y=0, z=0 and `x/a+y/b+z/c=1`
Evaluate `int_0^inftye^(x^3)/sqrtx dx`
Find the length of the curve `x=y^3/3+1/(4y)` from `y=1 to y=2`
Solve `(D^2+D)y=e^(4x)`
Evaluate `int_0^1 int_(x^2)^x xy(x+y)dydx.`
Solve `(4x+3y-4)dx+(3x-7y-3)dy=0`
Solve `dy/dx=1+xy` with initial condition `x_0=0,y_0=0.2` By Taylors series method. Find the approximate value of y for x= 0.4(step size = 0.4).
Solve `(d^2y)/dx^2-16y=x^2 e^(3x)+e^(2x)-cos3x+2^x`
Show that `int_0^pi log(1+acos x)/cos x dx=pi sin^-1 a 0 ≤ a ≤1.`
Evaluate `int int int (x+y+z)` `dxdydz ` over the tetrahedron bounded by the planes x = 0, y = 0, z = 0 and x + y + z = 1.
In a circuit containing inductance L, resistance R, and voltage E, the current i is given by `L (di)/dt+Ri=E`.Find the current i at time t at t = 0 and i = 0 and L, R and E are constants.
