Advertisements
Advertisements
Question
Find the ratio in which the point P(m, 6) divides the join of A(-4, 3) and B(2, 8) Also, find the value of m.
Solution
Let the point P(m,6) divide the line AB in the ratio k :.1
Then, by the section formula:
`x = (mx_2+nx_1)/(m+n) , y =(my_2+ny_1)/(m+n)`
The coordinates of P are (m,6).
`m = (2k-4)/(k+1) , 6 = (8k+3)/(k+1)`
⇒ m (k+1)= 2k-4,6k+6=8k+3
⇒m (k+1) = 2k -4 , 6-3= 8k-6k
⇒m(k+1) = 2k-4, 2k = 3
`⇒m(k+1) = 2k-4,k=3/2`
Therefore, the point P divides the line AB in the ratio 3:2
Now, putting the value of k in the equation m(k+1) = 2k-4 , we get:
`m(3/2+1) = 2(3/2)-4`
`⇒ m((3+2)/2) = 3-4`
` ⇒ (5m)/2 = -1 ⇒ 5m = -2 ⇒m=-2/5`
Therefore, the value of `m = -2/5`
So, the coordinates of P are `(-2/5,6).`
APPEARS IN
RELATED QUESTIONS
Find the third vertex of a triangle, if two of its vertices are at (−3, 1) and (0, −2) and the centroid is at the origin.
Prove that the points (3, 0), (4, 5), (-1, 4) and (-2, -1), taken in order, form a rhombus.
Also, find its area.
Determine the ratio in which the point P (m, 6) divides the join of A(-4, 3) and B(2, 8). Also, find the value of m.
Show that the points A(2,1), B(5,2), C(6,4) and D(3,3) are the angular points of a parallelogram. Is this figure a rectangle?
In what ratio does the point P(2,5) divide the join of A (8,2) and B(-6, 9)?
If the point `P (1/2,y)` lies on the line segment joining the points A(3, -5) and B(-7, 9) then find the ratio in which P divides AB. Also, find the value of y.
The base BC of an equilateral triangle ABC lies on y-axis. The coordinates of point C are (0, -3). The origin is the midpoint of the base. Find the coordinates of the points A and B. Also, find the coordinates of another point D such that ABCD is a rhombus.
In what ratio does the point C (4,5) divides the join of A (2,3) and B (7,8) ?
Find the centroid of the triangle whose vertices is (−2, 3) (2, −1) (4, 0) .
If A(−3, 5), B(−2, −7), C(1, −8) and D(6, 3) are the vertices of a quadrilateral ABCD, find its area.
If the points A (1,2) , O (0,0) and C (a,b) are collinear , then find a : b.
If A (2, 2), B (−4, −4) and C (5, −8) are the vertices of a triangle, than the length of the median through vertex C is
If A(4, 9), B(2, 3) and C(6, 5) are the vertices of ∆ABC, then the length of median through C is

In the above figure, seg PA, seg QB and RC are perpendicular to seg AC. From the information given in the figure, prove that: `1/x + 1/y = 1/z`
What are the coordinates of origin?
Point (–10, 0) lies ______.
Ordinate of all points on the x-axis is ______.
Assertion (A): The ratio in which the line segment joining (2, -3) and (5, 6) internally divided by x-axis is 1:2.
Reason (R): as formula for the internal division is `((mx_2 + nx_1)/(m + n) , (my_2 + ny_1)/(m + n))`
Ryan, from a very young age, was fascinated by the twinkling of stars and the vastness of space. He always dreamt of becoming an astronaut one day. So, he started to sketch his own rocket designs on the graph sheet. One such design is given below :
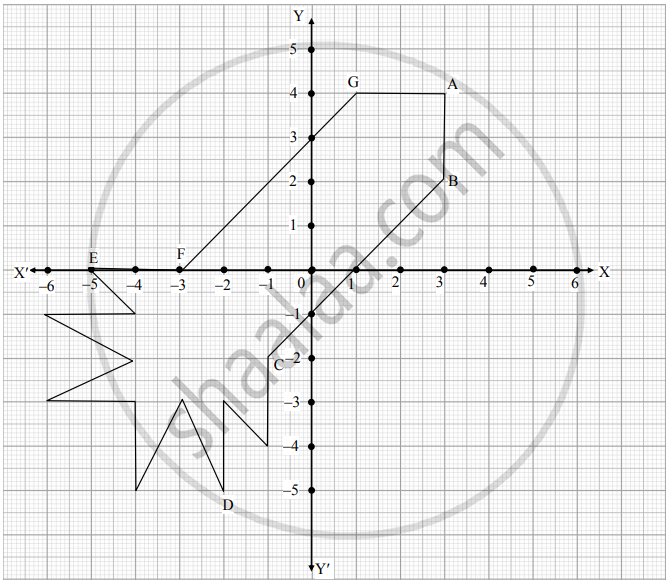
Based on the above, answer the following questions:
i. Find the mid-point of the segment joining F and G. (1)
ii. a. What is the distance between the points A and C? (2)
OR
b. Find the coordinates of the points which divides the line segment joining the points A and B in the ratio 1 : 3 internally. (2)
iii. What are the coordinates of the point D? (1)
