Question

If A(4, 9), B(2, 3) and C(6, 5) are the vertices of ∆ABC, then the length of median through C is

Options

• 5 units  

• \[\sqrt{10}\] units                      

   

• 25 units   

•  10 units  

Answer 1

It is given that A(4, 9), B(2, 3) and C(6, 5) are the vertices of ∆ABC. 

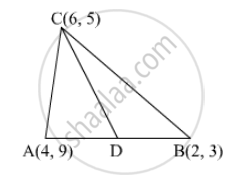
Let CD be the median of ∆ABC through C. Then, D is the mid-point of AB.

Using mid-point formula, we get

Coordinates of D = \[\left( \frac{4 + 2}{2}, \frac{9 + 3}{2} \right) = \left( \frac{6}{2}, \frac{12}{2} \right) = \left( 3, 6 \right)\]

∴ Length of the median, AD 

\[= \sqrt{\left( 6 - 3 \right)^2 + \left( 5 - 6 \right)^2} \left( \text{ Using distance formula } \right)\]
\[ = \sqrt{3^2 + \left( - 1 \right)^2}\]
\[ = \sqrt{10} \text{ units } \]

Thus, the length of the required median is \[\sqrt{10}\] units.