Advertisements
Advertisements
Question
Find the area of greatest rectangle that can be inscribed in an ellipse `x^2/"a"^2 + y^2/"b"^2` = 1
Solution
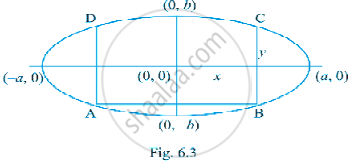
Let ABCD be the rectangle of maximum area with sides AB = 2x and BC = 2y
Where C (x, y) is a point on the ellipse `x^2/"a"^2 + y^2/"b"^2` = 1 as shown in the Fig.6.3.
The area A of the rectangle is 4xy
i.e. A = 4xy which gives A2 = 16x2y2 = s ....(say)
Therefore, s = `16x^2 (1 - x^2/"a"^2)*"b"^2`
= `(16"b"^2)/"a"^2 ("a"^2x^2 - x^4)`
⇒ `"ds"/"dx" = (16"b"^2)/"a"^2 * [2"a"^2x - 4x^3]`
Again, `"ds"/"dx"` = 0
⇒ x = `"a"/sqrt(2)` nad y = `"b"/sqrt(2)`
Now, `("d"^2"s")/("dx"^2) = (16"b"^2)/"a"^2 [2"a"^2 - 12x^2]`
At x = `"a"/sqrt(2), ("d"^2"s")/("dx"^2)`
= `(16"b"^2)/"a"^2 [2"a"^2 - 6"a"^2]`
= `(16"b"^2)/"a"62 (-4"a"^2) < 0`
Thus at x = `"a"/sqrt(2)`, y = `"b"/sqrt(2)`
s is maximum and hence the area A is maximum.
Maximum area = 4.x.y
= `4 * "a"/sqrt(2) * "b"/sqrt(2)`
= 2ab sq units.
APPEARS IN
RELATED QUESTIONS
f (x) = 2x2 − 5x + 3 on [1, 3] Discuss the applicability of Rolle's theorem for the following function on the indicated intervals ?
Verify Rolle's theorem for the following function on the indicated interval f (x) = (x − 1) (x − 2)2 on [1, 2] ?
Verify Rolle's theorem for the following function on the indicated interval f (x) = x(x − 1)2 on [0, 1] ?
Verify Rolle's theorem for the following function on the indicated interval f (x) = (x2 − 1) (x − 2) on [−1, 2] ?
Verify Rolle's theorem for the following function on the indicated interval f (x) = x(x − 4)2 on the interval [0, 4] ?
Verify Rolle's theorem for each of the following function on the indicated interval f (x) = cos 2 (x − π/4) on [0, π/2] ?
Verify Rolle's theorem for the following function on the indicated interval \[f\left( x \right) = \frac{x}{2} - \sin\frac{\pi x}{6} \text { on }[ - 1, 0]\]?
Verify Rolle's theorem for the following function on the indicated interval f(x) = sin x − sin 2x on [0, π]?
At what point on the following curve, is the tangent parallel to x-axis y = x2 on [−2, 2]
?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem f(x) = 2x − x2 on [0, 1] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theore f(x) = tan−1 x on [0, 1] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem f(x) = x2 + x − 1 on [0, 4] ?
Find the points on the curve y = x3 − 3x, where the tangent to the curve is parallel to the chord joining (1, −2) and (2, 2) ?
Find a point on the curve y = x3 + 1 where the tangent is parallel to the chord joining (1, 2) and (3, 28) ?
If the value of c prescribed in Rolle's theorem for the function f (x) = 2x (x − 3)n on the interval \[[0, 2\sqrt{3}] \text { is } \frac{3}{4},\] write the value of n (a positive integer) ?
For the function f (x) = x + \[\frac{1}{x}\] ∈ [1, 3], the value of c for the Lagrange's mean value theorem is
The value of c in Rolle's theorem for the function \[f\left( x \right) = \frac{x\left( x + 1 \right)}{e^x}\] defined on [−1, 0] is
The value of c in Rolle's theorem for the function f (x) = x3 − 3x in the interval [0,\[\sqrt{3}\]] is
Show that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi-vertical angle α is one-third that of the cone and the greatest volume of the cylinder is `(4)/(27) pi"h"^3 tan^2 α`.
If f(x) = `1/(4x^2 + 2x + 1)`, then its maximum value is ______.
At what point, the slope of the curve y = – x3 + 3x2 + 9x – 27 is maximum? Also find the maximum slope.
It is given that at x = 1, the function x4 - 62x2 + ax + 9 attains its maximum value on the interval [0, 2]. Find the value of a.
If f(x) = ax2 + 6x + 5 attains its maximum value at x = 1, then the value of a is
The minimum value of `1/x log x` in the interval `[2, oo]` is
The function f(x) = [x], where [x] =greater integer of x, is
