Advertisements
Advertisements
प्रश्न
Find the area of greatest rectangle that can be inscribed in an ellipse `x^2/"a"^2 + y^2/"b"^2` = 1
उत्तर
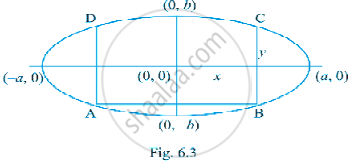
Let ABCD be the rectangle of maximum area with sides AB = 2x and BC = 2y
Where C (x, y) is a point on the ellipse `x^2/"a"^2 + y^2/"b"^2` = 1 as shown in the Fig.6.3.
The area A of the rectangle is 4xy
i.e. A = 4xy which gives A2 = 16x2y2 = s ....(say)
Therefore, s = `16x^2 (1 - x^2/"a"^2)*"b"^2`
= `(16"b"^2)/"a"^2 ("a"^2x^2 - x^4)`
⇒ `"ds"/"dx" = (16"b"^2)/"a"^2 * [2"a"^2x - 4x^3]`
Again, `"ds"/"dx"` = 0
⇒ x = `"a"/sqrt(2)` nad y = `"b"/sqrt(2)`
Now, `("d"^2"s")/("dx"^2) = (16"b"^2)/"a"^2 [2"a"^2 - 12x^2]`
At x = `"a"/sqrt(2), ("d"^2"s")/("dx"^2)`
= `(16"b"^2)/"a"^2 [2"a"^2 - 6"a"^2]`
= `(16"b"^2)/"a"62 (-4"a"^2) < 0`
Thus at x = `"a"/sqrt(2)`, y = `"b"/sqrt(2)`
s is maximum and hence the area A is maximum.
Maximum area = 4.x.y
= `4 * "a"/sqrt(2) * "b"/sqrt(2)`
= 2ab sq units.
APPEARS IN
संबंधित प्रश्न
Find the local maxima and local minima, of the function f(x) = sin x − cos x, 0 < x < 2π.
A cone is inscribed in a sphere of radius 12 cm. If the volume of the cone is maximum, find its height
f(x) = 3 + (x − 2)2/3 on [1, 3] Discuss the applicability of Rolle's theorem for the following function on the indicated intervals ?
\[f\left( x \right) = \begin{cases}- 4x + 5, & 0 \leq x \leq 1 \\ 2x - 3, & 1 < x \leq 2\end{cases}\] Discuss the applicability of Rolle's theorem for the following function on the indicated intervals ?
Verify Rolle's theorem for the following function on the indicated interval f(x) = x2 − 8x + 12 on [2, 6] ?
Verify Rolle's theorem for the following function on the indicated interval f (x) = x2 + 5x + 6 on the interval [−3, −2] ?
Verify Rolle's theorem for the following function on the indicated interval f(x) = sin 2x on [0, π/2] ?
Verify Rolle's theorem for the following function on the indicated interval f(x) = cos 2x on [−π/4, π/4] ?
Verify Rolle's theorem for the following function on the indicated interval f(x) = ex sin x on [0, π] ?
Verify Rolle's theorem for the following function on the indicated interval f(x) = ex cos x on [−π/2, π/2] ?
Verify Rolle's theorem for the following function on the indicated interval f(x) = 2 sin x + sin 2x on [0, π] ?
Verify Rolle's theorem for the following function on the indicated interval \[f\left( x \right) = \frac{x}{2} - \sin\frac{\pi x}{6} \text { on }[ - 1, 0]\]?
If f : [−5, 5] → R is differentiable and if f' (x) doesnot vanish anywhere, then prove that f (−5) ± f (5) ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem f(x) = 2x2 − 3x + 1 on [1, 3] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem f(x) = x2 − 2x + 4 on [1, 5] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem \[f\left( x \right) = x + \frac{1}{x} \text { on }[1, 3]\] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem f(x) = sin x − sin 2x − x on [0, π] ?
Find a point on the curve y = x2 + x, where the tangent is parallel to the chord joining (0, 0) and (1, 2) ?
Find a point on the parabola y = (x − 3)2, where the tangent is parallel to the chord joining (3, 0) and (4, 1) ?
If the value of c prescribed in Rolle's theorem for the function f (x) = 2x (x − 3)n on the interval \[[0, 2\sqrt{3}] \text { is } \frac{3}{4},\] write the value of n (a positive integer) ?
Rolle's theorem is applicable in case of ϕ (x) = asin x, a > a in
If f (x) = ex sin x in [0, π], then c in Rolle's theorem is
A company manufactures two types of novelty souvenirs made of plywood. Souvenirs of types A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 4 hours available for assembling. The profit is ₹ 50 each for type A and ₹60 each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize profit? Formulate the above LPP and solve it graphically and find the maximum profit.
Show that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi-vertical angle α is one-third that of the cone and the greatest volume of the cylinder is `(4)/(27) pi"h"^3 tan^2 α`.
Find the difference between the greatest and least values of the function f(x) = sin2x – x, on `[- pi/2, pi/2]`
An isosceles triangle of vertical angle 2θ is inscribed in a circle of radius a. Show that the area of triangle is maximum when θ = `pi/6`
At x = `(5pi)/6`, f(x) = 2 sin3x + 3 cos3x is ______.
The minimum value of `1/x log x` in the interval `[2, oo]` is
