Advertisements
Advertisements
Question
Show that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi-vertical angle α is one-third that of the cone and the greatest volume of the cylinder is `(4)/(27) pi"h"^3 tan^2 α`.
Solution
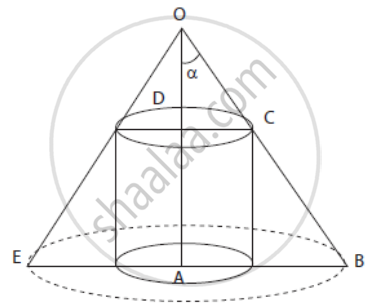
Let CD = R, AD = x
⇒ OD = h - x
∵ ODC ∼ ΔOAB
⇒ `(h - x)/h = R/"AB" ⇒ (h - x)/h = R/(h tan α)`
⇒ R = (h - x) tan α
V = πR2x
= π(h - x)2 tan2α. x
= π tan2α (h - x)2x
`dV/dx = π tan2α (h2 - 4hx + 3x2)`
`dV/dx = 0 = h^2 - 4hx + 3x^2 = 0`
⇒ (h - x)(h - 3x) = 0
⇒ x = h (not possible ) or x =` h/3`
`(d^2V)/(dx^2) = π tan^2α (-4h + 6x)`
`((d^2V)/(dx^2))_(x = h/3) = π tan^2α (-2h) < 0`
⇒ V is maximum for x = `h/3`.
So, Vmax = π tan2α (h - x)2x
`= π tan^2α ( h - h/3 )^2 h/3`
= `(4πh)^3/27 tan^2 a`
APPEARS IN
RELATED QUESTIONS
Find the absolute maximum and absolute minimum values of the function f given by f(x)=sin2x-cosx,x ∈ (0,π)
A cylindrical tank of radius 10 m is being filled with wheat at the rate of 314 cubic metre per hour. Then the depth of the wheat is increasing at the rate of ______.
f(x) = 3 + (x − 2)2/3 on [1, 3] Discuss the applicability of Rolle's theorem for the following function on the indicated intervals ?
\[f\left( x \right) = \begin{cases}- 4x + 5, & 0 \leq x \leq 1 \\ 2x - 3, & 1 < x \leq 2\end{cases}\] Discuss the applicability of Rolle's theorem for the following function on the indicated intervals ?
Verify Rolle's theorem for the following function on the indicated interval f (x) = (x2 − 1) (x − 2) on [−1, 2] ?
Verify Rolle's theorem for the following function on the indicated interval f (x) = x2 + 5x + 6 on the interval [−3, −2] ?
Verify Rolle's theorem for the following function on the indicated interval f(x) = sin 2x on [0, π/2] ?
Verify Rolle's theorem for the following function on the indicated interval f (x) = \[{e^{1 - x}}^2\] on [−1, 1] ?
Examine if Rolle's theorem is applicable to any one of the following functions.
(i) f (x) = [x] for x ∈ [5, 9]
(ii) f (x) = [x] for x ∈ [−2, 2]
Can you say something about the converse of Rolle's Theorem from these functions?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem f(x) = x(x −1) on [1, 2] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem f(x) = 2x2 − 3x + 1 on [1, 3] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem f(x) = x2 − 2x + 4 on [1, 5] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theore f(x) = (x − 1)(x − 2)(x − 3) on [0, 4] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem \[f\left( x \right) = x + \frac{1}{x} \text { on }[1, 3]\] ?
Find a point on the parabola y = (x − 3)2, where the tangent is parallel to the chord joining (3, 0) and (4, 1) ?
Let C be a curve defined parametrically as \[x = a \cos^3 \theta, y = a \sin^3 \theta, 0 \leq \theta \leq \frac{\pi}{2}\] . Determine a point P on C, where the tangent to C is parallel to the chord joining the points (a, 0) and (0, a).
Using Lagrange's mean value theorem, prove that (b − a) sec2 a < tan b − tan a < (b − a) sec2 b
where 0 < a < b < \[\frac{\pi}{2}\] ?
If 4a + 2b + c = 0, then the equation 3ax2 + 2bx + c = 0 has at least one real root lying in the interval
The value of c in Rolle's theorem for the function \[f\left( x \right) = \frac{x\left( x + 1 \right)}{e^x}\] defined on [−1, 0] is
The value of c in Lagrange's mean value theorem for the function f (x) = x (x − 2) when x ∈ [1, 2] is
Find the maximum and minimum values of f(x) = secx + log cos2x, 0 < x < 2π
An isosceles triangle of vertical angle 2θ is inscribed in a circle of radius a. Show that the area of triangle is maximum when θ = `pi/6`
At what point, the slope of the curve y = – x3 + 3x2 + 9x – 27 is maximum? Also find the maximum slope.
The least value of the function f(x) = `"a"x + "b"/x` (where a > 0, b > 0, x > 0) is ______.
The least value of the function f(x) = 2 cos x + x in the closed interval `[0, π/2]` is:
If f(x) = ax2 + 6x + 5 attains its maximum value at x = 1, then the value of a is
