Advertisements
Advertisements
Question
An isosceles triangle of vertical angle 2θ is inscribed in a circle of radius a. Show that the area of triangle is maximum when θ = `pi/6`
Solution
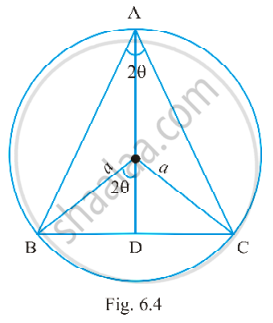
Let ABC be an isosceles triangle inscribed in the circle with radius a such that AB = AC.
AD = AO + OD = a + a cos2θ and BC = 2BD = 2a sin2θ (see fig. 16.4)
Therefore, area of the triangle ABC
i.e. ∆ = `1/2` BC . AD
= `1/2 2"a" sin2theta * ("a" + "a" cos2theta)`
= a2sin2θ (1 + cos2θ)
⇒ ∆ = `"a"^2sin2theta + 1/2 "a"^2 sin4theta`
Therefore, `("d"∆)/("d"theta)` = 2a2cos2θ + 2a2cos4θ
= 2a2(cos2θ + cos4θ)
`("d"∆)/("d"theta)` = cos2θ = –cos4θ = cos (π – 4θ)
Therefore, 2θ = π – 4θ
⇒ θ = `pi/6`
`("d"^2∆)/("d"theta)` = 2a2 (–2sin2θ – 4sin4θ) < 0 `("at" theta = pi/6)`.
Therefore, Area of triangle is maximum when θ = `pi/6`.
APPEARS IN
RELATED QUESTIONS
f (x) = [x] for −1 ≤ x ≤ 1, where [x] denotes the greatest integer not exceeding x Discuss the applicability of Rolle's theorem for the following function on the indicated intervals ?
f (x) = x2/3 on [−1, 1] Discuss the applicability of Rolle's theorem for the following function on the indicated intervals ?
Verify Rolle's theorem for the following function on the indicated interval f (x) = x(x − 4)2 on the interval [0, 4] ?
Verify Rolle's theorem for the following function on the indicated interval f (x) = x2 + 5x + 6 on the interval [−3, −2] ?
Verify Rolle's theorem for the following function on the indicated interval f (x) = \[{e^{1 - x}}^2\] on [−1, 1] ?
Verify Rolle's theorem for the following function on the indicated interval f (x) = log (x2 + 2) − log 3 on [−1, 1] ?
Verify Rolle's theorem for the following function on the indicated interval f(x) = sin x + cos x on [0, π/2] ?
Verify Rolle's theorem for the following function on the indicated interval f(x) = 2 sin x + sin 2x on [0, π] ?
Verify Rolle's theorem for the following function on the indicated interval f(x) = 4sin x on [0, π] ?
If f : [−5, 5] → R is differentiable and if f' (x) doesnot vanish anywhere, then prove that f (−5) ± f (5) ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem f(x) = x2 − 3x + 2 on [−1, 2] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem f(x) = x2 − 2x + 4 on [1, 5] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem f(x) = 2x − x2 on [0, 1] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem \[f\left( x \right) = x + \frac{1}{x} \text { on }[1, 3]\] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem f(x) = x(x + 4)2 on [0, 4] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem \[f\left( x \right) = \sqrt{x^2 - 4} \text { on }[2, 4]\] ?
The value of c in Rolle's theorem for the function \[f\left( x \right) = \frac{x\left( x + 1 \right)}{e^x}\] defined on [−1, 0] is
Find the points on the curve x2 + y2 − 2x − 3 = 0 at which the tangents are parallel to the x-axis ?
A wire of length 50 m is cut into two pieces. One piece of the wire is bent in the shape of a square and the other in the shape of a circle. What should be the length of each piece so that the combined area of the two is minimum?
Show that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi-vertical angle α is one-third that of the cone and the greatest volume of the cylinder is `(4)/(27) pi"h"^3 tan^2 α`.
Show that the local maximum value of `x + 1/x` is less than local minimum value.
At what point, the slope of the curve y = – x3 + 3x2 + 9x – 27 is maximum? Also find the maximum slope.
The least value of the function f(x) = `"a"x + "b"/x` (where a > 0, b > 0, x > 0) is ______.
The least value of the function f(x) = 2 cos x + x in the closed interval `[0, π/2]` is:
The minimum value of `1/x log x` in the interval `[2, oo]` is
