Advertisements
Advertisements
Question
Find the arithmetic mean (correct to the nearest whole number) by using step-deviation method.
| x | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| f | 20 | 43 | 75 | 67 | 72 | 45 | 39 | 9 | 8 | 6 |
Solution
Let the assumed mean = 30
|
x |
f |
d = x – A A = 30 |
`bb(t = (x - A)/i` `bb(= (x - 30)/5)` |
ft |
| 5 | 20 | –25 | –5 | –100 |
| 10 | 43 | –20 | –4 | –172 |
| 15 | 75 | –15 | –3 | –225 |
| 20 | 67 | –10 | –2 | –134 |
| 25 | 72 | –5 | –1 | –72 |
| 30 | 45 | 0 | 0 | 0 |
| 35 | 39 | 5 | 1 | 39 |
| 40 | 9 | 10 | 2 | 18 |
| 45 | 8 | 15 | 3 | 24 |
| 50 | 6 | 20 | 4 | 24 |
| Σf = 384 | Σft = –598 |
By step deviation method, we have
Mean = `A + (Σft)/(Σf) xx i`
= `(30 + (598) xx 5)/384`
= `30 + (-598)/384 xx 5`
= 30 – 7.79
= 22.21
= 22 (appx.) [To nearest whole number]
APPEARS IN
RELATED QUESTIONS
The following table gives the weekly wages of workers in a factory.
| Weekly wages (Rs) | No. of workers |
| 50 – 55 | 5 |
| 55 – 60 | 20 |
| 60 – 65 | 10 |
| 65 – 70 | 10 |
| 70 – 75 | 9 |
| 75 – 80 | 6 |
| 80 – 85 | 12 |
| 85 – 90 | 8 |
Calculate the mean by using:
Short-cut method
The following are the marks obtained by 70 boys in a class test:
| Marks | No. of boys |
| 30 – 40 | 10 |
| 40 – 50 | 12 |
| 50 – 60 | 14 |
| 60 – 70 | 12 |
| 70 – 80 | 9 |
| 80 – 90 | 7 |
| 90 – 100 | 6 |
Calculate the mean by:
Step-deviation method
The mean of the following distribution is `21 1/7`. Find the value of ‘f’.
| C.I. | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
| Frequency | 8 | 22 | 31 | f | 2 |
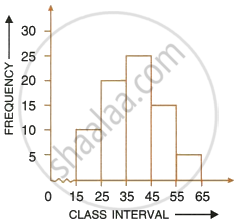
Using the information given in the adjoining histogram, calculate the mean.
Find the mean, median and mode of the following marks obtained by 16 students in a class test marked out of 10 marks:
0, 0, 2, 2, 3, 3, 3, 4, 5, 5, 5, 5, 6, 6, 7 and 8.
In a malaria epidemic, the number of cases diagnosed were as follows:
| Date July | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Num | 5 | 12 | 20 | 27 | 46 | 30 | 31 | 18 | 11 | 5 | 0 | 1 |
On what days do the mode and upper and lower quartiles occur?
If the mean of 8 , 14 , 20 , x and 12 is 13, find x.
Find the mode of the following:
15, 17, 16, 17, 10, 12, 14, 16, 19, 12, 16, 15, 16
Find the median of the given values : 47, 53, 62, 71, 83, 21, 43, 47, 41
The median first 6 odd natural numbers is ____________
