Question

Find the co-ordinates of the orthocenter of the triangle whose vertices are A(3, –2), B(7, 6), C(–1, 2).

Answer 1

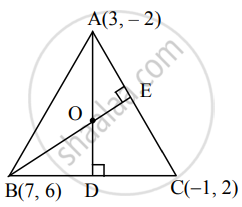
Let O be the orthocentre of ΔABC.

Let AD and BE be the altitudes on the sides BC and AC respectively.

Slope of side BC = `(2 - 6)/(-1 - 7) = (-4)/(-8) = 1/2`

∴ Slope of AD = – 2   ...[∵ AD ⊥ BC]

∴ Equation of line AD is

y – (– 2) = (– 2) (x – 3)

∴ y + 2 = – 2x + 6

∴ 2x + y – 4 = 0  .....(i)

Slope of side AC = `(-2 - 2)/(3 - (-1)) = (-4)/4` = – 1

∴ Slope of BE = 1  ...[∵ BE ⊥ AC]

∴ Equation of line BE is

y – 6 = 1(x – 7)

∴ y – 6 = x – 7

∴ x = y + 1 .....(ii)

Substituting x = y + 1 in (i), we get

2(y + 1) + y – 4 = 0

∴ 2y + 2 + y – 4 = 0

∴ 3y – 2 = 0

∴ y = `2/3`

Substituting y = `2/3` in (ii), we get

x = `2/3 + 1 = 5/3`

∴ Co-ordinates of orthocentre, O = `(5/3, 2/3)`