Advertisements
Advertisements
Question
D(−1, 8), E(4, −2), F(−5, −3) are midpoints of sides BC, CA and AB of ∆ABC Find co-ordinates of the circumcenter of ΔABC
Solution
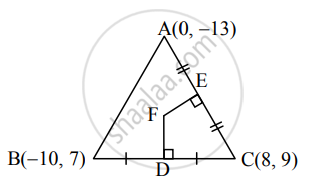
Here, A(0, −13), B(−10, 7), C(8, 9) are the vertices of ΔABC.
Let F be the circumcentre of ΔABC.
Let FD and FE be perpendicular bisectors of the sides BC and AC respectively.
∴ D and E are the midpoints of side BC and AC.
∴ D ≡ `((-10 + 8)/2, (7 + 9)/2)`
∴ D = (−1, 8)
and E ≡ `((0 + 8)/2, (-13 + 9)/2)`
∴ E = (4, −2)
Now, slope of BC = `(7 - 9)/(-10 - 8) = 1/9`
∴ Slope of FD = − 9 ...[∵ FD ⊥ BC]
Since FD passes through (−1, 8) and has slope −9, equation of FD is
y − 8 = −9(x + 1)
∴ y − 8 = −9x − 9
∴ y = −9x − 1 ...(i)
Also, slope of AC = `(-13 - 9)/(0 - 8) = 11/4`
∴ Slope of FE = `(-4)/11` ...[∵ FE ⊥ AC]
Since FE passes through (4, −2) and has slope `(-4)/11`, equation of FE is
y + 2 = `(-4)/11(x - 4)`
∴ 11(y + 2) = −4(x − 4)
∴ 11y + 22 = −4x + 16
∴ 4x + 11y = − 6 ...(ii)
To find coordinates of circumcentre, we have to solve equations (i) and (ii).
Substituting the value of y in (ii), we get
4x + 11(−9x − 1) = − 6
∴ 4x − 99x − 11 = − 6
∴ −95x = 5
∴ x = `(-1)/19`
Substituting the value of x in (i), we get
y = `-9((-1)/19) - 1 = (-10)/19`
∴ Co-ordinates of circumcentre F ≡ `((-1)/19, (-10)/19)`.
APPEARS IN
RELATED QUESTIONS
Find the slope, X-intercept, Y-intercept of the following line:
2x + 3y – 6 = 0
Find the slope, X-intercept, Y-intercept of the following line:
x + 2y = 0
Write the following equation in ax + by + c = 0 form.
y = 4
Write the following equation in ax + by + c = 0 form.
`x/2 + y/4` = 1
Write the following equation in ax + by + c = 0 form.
`x/3 - y/2` = 0
Show that lines x − 2y − 7 = 0 and 2x + y + 1 = 0 are perpendicular to each other. Find their point of intersection
If the line 3x + 4y = p makes a triangle of area 24 square unit with the co-ordinate axes then find the value of p.
Find the co-ordinates of the foot of the perpendicular drawn from the point A(–2, 3) to the line 3x – y – 1 = 0
Find the co-ordinates of the circumcenter of the triangle whose vertices are A(–2, 3), B(6, –1), C(4, 3).
Find the co-ordinates of the orthocenter of the triangle whose vertices are A(3, –2), B(7, 6), C(–1, 2).
Find the equation of the line whose X-intercept is 3 and which is perpendicular to the line 3x − y + 23 = 0.
Find the distance of the point A(−2, 3) from the line 12x − 5y − 13 = 0
Find the distance between parallel lines 9x + 6y − 7 = 0 and 3x + 2y + 6 = 0
Find points on the line x + y − 4 = 0 which are at one unit distance from the line 4x + 3y – 10 = 0.
O(0, 0), A(6, 0) and B(0, 8) are vertices of a triangle. Find the co-ordinates of the incenter of ∆OAB
Select the correct option from the given alternatives:
If A(1, −2), B(−2, 3) and C(2, −5) are the vertices of ∆ABC, then the equation of the median BE is
Select the correct option from the given alternatives:
The equation of a line, having inclination 120° with positive direction of X−axis, which is at a distance of 3 units from the origin is
Select the correct option from the given alternatives:
Distance between the two parallel lines y = 2x + 7 and y = 2x + 5 is
Answer the following question:
Find the distance of the origin from the line x = – 2
Answer the following question:
Which of the following lines passes through the origin?
Answer the following question:
Obtain the equation of the line which is parallel to the Y−axis and 2 units to the left of it.
Answer the following question:
Obtain the equation of the line which is parallel to the Y−axis and making an intercept of 3 on the X−axis.
Answer the following question:
Find the equation of the line which passes through the point of intersection of lines x + y − 3 = 0, 2x − y + 1 = 0 and which is parallel X-axis
Answer the following question:
Find the equation of the line which passes through the point of intersection of lines x + y + 9 = 0, 2x + 3y + 1 = 0 and which makes X-intercept 1.
Answer the following question:
Find points on the X-axis whose distance from the line `x/3 + y/4` = 1 is 4 unit
A particle is moving in a straight line according to as S = 24t + 3t2 - t3, then the time it will come to rest is ______
Let the straight line x = b divide the area enclosed by y = (1 - x)2, y = 0 and x = 0 into two parts R1(0 ≤ x ≤ b) and R2 (b ≤ x ≤ 1) such that `R_1 - R_2 = 1/4`. Then b equals ______
The equation 12x2 + 7xy + ay2 + 13x - y + 3 = 0 represents a pair of perpendicular lines. Then the value of 'a' is ______
If a plane has x-intercept l, y-intercept m and z-intercept n, and perpendicular distance of plane from the origin is k, then _______.
The length of the perpendicular from the origin on the line `(xsinalpha)/"b" - (ycosalpha)/"a" - 1 = 0` is ______.
If the distance of the point (1, 1, 1) from the origin is half its distance from the plane x + y + z + k = 0, then k = ______.
Find the distance of the origin from the line 7x + 24y – 50 = 0 is:
