Advertisements
Advertisements
Question
Find the mid-point of the line segment joining the points
`(1/2, (-3)/7)` and `(3/2, (-11)/7)`
Solution

Mid−point of AB = `((1/2 + 3/2)/2, ((-3)/7 - 11/7)/2)`
= `((4/2)/2, ((-14)/7)/2)`
= `(2/2, (-2)/2)`
= (1, −1)
APPEARS IN
RELATED QUESTIONS
ABCD is a parallelogram where A(x, y), B(5, 8), C(4, 7) and D(2, -4). Find
1) Coordinates of A
2) An equation of diagonal BD
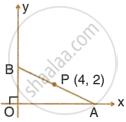
In the given figure, P(4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
P(4, 2) and Q(–1, 5) are the vertices of parallelogram PQRS and (–3, 2) are the co-ordinates of the point of intersection of its diagonals. Find co-ordinates of R and S.
A(5, x), B(−4, 3) and C(y, –2) are the vertices of the triangle ABC whose centroid is the origin. Calculate the values of x and y.
Find the coordinates of midpoint of the segment joining the points (22, 20) and (0, 16).
P( -2, 5), Q(3, 6 ), R( -4, 3) and S(-9, 2) are the vertices of a quadrilateral. Find the coordinates of the midpoints of the diagonals PR and QS. Give a special name to the quadrilateral.
Find the centroid of a triangle whose vertices are (3, -5), (-7, 4) and ( 10, -2).
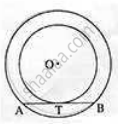
As shown in the figure. two concentric circles are given and line AB is the tangent to the smaller circle at T. Shown that T is the midpoint of Seg AB
The points A(−3, 6), B(0, 7) and C(1, 9) are the mid-points of the sides DE, EF and FD of a triangle DEF. Show that the quadrilateral ABCD is a parallelogram.
Find coordinates of midpoint of segment joining (– 2, 6) and (8, 2)
