Advertisements
Advertisements
Question
Find the zeroes of the polynomial `x^2 + x – p(p + 1) `
Solution
f(x) = x2 + x – p (p + 1)
By adding and subtracting px, we get
`f(x) = x^2 + px + x – px – p(p + 1)`
= `x^2 + (p + 1) x – px –p (p + 1)`
=` x[x + (p + 1)] –p [x + (p + 1)]`
= `[x + (p + 1)] (x – p)`
`f(x) = 0`
⇒`[x + (p + 1)] (x – p) = 0`
⇒ `[x + (p + 1)] = 0 or (x – p) = 0`
⇒ `x = – (p + 1) or x = p`
So, the zeroes of f(x) are – (p + 1) and p.
APPEARS IN
RELATED QUESTIONS
The graphs of y = p(x) are given in following figure, for some polynomials p(x). Find the number of zeroes of p(x).
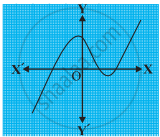
The graphs of y = p(x) are given in following figure, for some polynomials p(x). Find the number of zeroes of p(x).
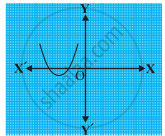
Find the zeroes of the polynomial `x^2 – 3x – m(m + 3)`
If 𝛼, 𝛽 are the zeroes of the polynomial `f(x) = x^2 – 5x + k` such that 𝛼 - 𝛽 = 1, find the value of k = ?
A polynomial of degree n has ______.
If f(x) = 5x - 10 is divided by x – `sqrt2`, then the remainder will be ______.
If the graph of a polynomial intersects the x-axis at only one point, it cannot be a quadratic polynomial.
The zeroes of the quadratic polynomial x2 + kx + k, k ≠ 0 ______.
The graph of y = f(x) is shown in the figure for some polynomial f(x).
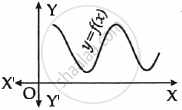
The number of zeroes of f(x) is ______.
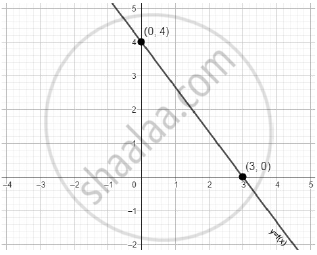
The given linear polynomial y = f(x) has