Advertisements
Advertisements
Question
For what value of k, is 3 a zero of the polynomial 2x2 + x + k?
Solution
We know that if `x = a` is zero polynomial, and then x - a is a factor of f(x)
Since 3 is zero of f (x)
Therefore x - 3 is a factor of f(x)
Now, we divide `f(x)=2x^2+ x+ k` by `g (x) = x-3` to find the value of k

Now, remainder = 0
`k + 21 = 0 `
` k = -21`
Hence, the value of k is = -21
APPEARS IN
RELATED QUESTIONS
Classify the following polynomials as linear, quadratic, cubic and biquadratic polynomials:
`t^2+1`
The sum and product of the zeros of a quadratic polynomial are \[- \frac{1}{2}\] and −3 respectively. What is the quadratic polynomial.
Write a quadratic polynomial, sum of whose zeros is \[2\sqrt{3}\] and their product is 2.
If α, β are the zeros of polynomial f(x) = x2 − p (x + 1) − c, then (α + 1) (β + 1) =
State whether the given algebraic expression are polynomial? Justify.
`2 - 5 sqrt x`
Divide. Write the quotient and the remainder.
(2y3 + 4y2 + 3) ÷ 2y2
Which of the following is not the graph of quadratic polynomial?
The below picture are few natural examples of parabolic shape which is represented by a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola. In structures, their curve represents an efficient method of load, and so can be found in bridges and in architecture in a variety of forms.




If α and `1/α` are the zeroes of the quadratic 2x2 − x + 8k, polynomial 2 then k is:
Basketball and soccer are played with a spherical ball. Even though an athlete dribbles the ball in both sports, a basketball player uses his hands and a soccer player uses his feet. Usually, soccer is played outdoors on a large field and basketball is played indoor on a court made out of wood. The projectile (path traced) of soccer ball and basketball are in the form of parabola representing quadratic polynomial.

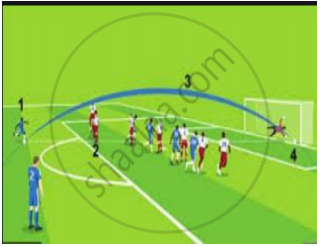
Observe the following graph and answer.
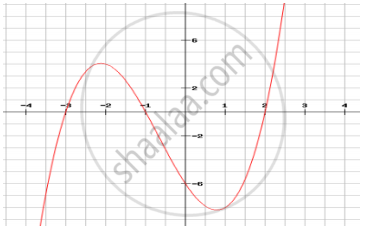
In the above graph, how many zeroes are there for the polynomial?
Degree of the polynomial 4x4 + 0x3 + 0x5 + 5x + 7 is ______.
