Advertisements
Advertisements
Question
For which of the following does the centre of mass lie outside the body?
Options
A pencil
A shotput
A dice
A bangle
Solution
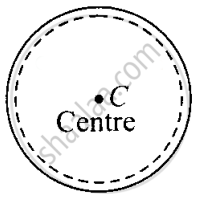
A bangle
Explanation:
The Center of mass of a system (body) is a point that moves as though all the mass were concentrated there and all external forces were applied there.
Important points about the center of Mass:
(i) The position of center of mass is independent of the coordinate system chosen.
(ii) The position of center of mass depends upon the shape of the body and the distribution of mass.
Example: The center of mass of a circular disc is within the material of the body while that of a circular ring is outside the material of the body.
(iii) We can imagine a rigid body also as a system of masses and hence every rigid body has a center of mass. In the case of a regularly shaped uniform rigid body, center of mass is simply the geometric centre of the body.
A bangle is in the form of a ring as shown in the diagram below. We know that the position of center of mass depends upon the shape of the body and the distribution of mass. So, out of four given bodies, the centre of mass lies at the centre, which is outside the body (boundary) whereas in all other three bodies it lies within the body because they are completely solid.
APPEARS IN
RELATED QUESTIONS
The centre of mass is defined as \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\]. Suppose we define "centre of charge" as \[\vec{R}_c = \frac{1}{Q} \sum_i q_i \vec{r_i}\] where qi represents the ith charge placed at \[\vec{r}_i\] and Q is the total charge of the system.
(a) Can the centre of charge of a two-charge system be outside the line segment joining the charges?
(b) If all the charges of a system are in X-Y plane, is it necessary that the centre of charge be in X-Y plane?
(c) If all the charges of a system lie in a cube, is it necessary that the centre of charge be in the cube?
Consider the following two statements:
(A) Linear momentum of the system remains constant.
(B) Centre of mass of the system remains at rest.
Two balls are thrown simultaneously in air. The acceleration of the centre of mass of the two balls while in air
The axis of rotation of a purely rotating body
(a) must pass through the centre of mass
(b) may pass through the centre of mass
(c) must pass through a particle of the body
(d) may pass through a particle of the body.
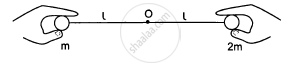
Two balls having masses m and 2m are fastened to two light strings of same length l (See figure). The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a) Find the velocity of the balls just after their collision. (b) How high will the ball rise after the collision?
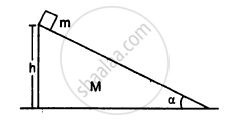
A block of mass m is placed on a triangular block of mass M which in turn is placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
Solve the following problem.
Four uniform solid cubes of edges 10 cm, 20 cm, 30 cm and 40 cm are kept on the ground, touching each other in order. Locate centre of mass of their system.
Solve the following problem.
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the center of the sphere while the other is at the boundary. Locate center of mass of the remaining sphere.
A shell of mass 'M' initially at rest suddenly explodes in three fragments. Two of these fragments are of mass 'M/4' each, which move with velocities 3 ms-1 and 4 ms-1 respectively in mutually perpendicular directions. The magnitude of velocity of the third fragment is ______.
A uniform square plate S (side c) and a uniform rectangular plate R (sides b, a) have identical areas and masses (Figure).
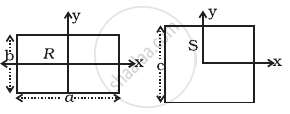
Show that
- IxR/IxS < 1
- IyR/IyS > 1
- IzR/IzS > 1
