Advertisements
Advertisements
Question
From differential equation of linear S.H.M., obtain an expression for acceleration, velocity and displacement of a particle performing S.H.M.
Solution
The differential equation of linear SHM is
`(d^2x)/dt^2+k/mx=0`
where m = mass of the particle performing SHM,
`(d^2x)/dt^2=`acceleration of the particle when its displacement from the mean position is x and k = force constant.
`(d^2x)/dt^2+k/mx=0`
Let `k/m = ω ^2`
∴ `(d^2x)/dt^2+ω ^2x=0`
∴ Acceleration, `a = (d^2x)/dt^2= -ω ^2x`..................(1 )
The minus sign shows that the acceleration and the displacement have opposite directions. Writing `nu= dx/dt `as the velocity of the particle.
`a= (d^2x)/dt^2 = (dnu)/dt=(dnu)/dx. (dx)/(dt)=(dnu)/dx.nu=nu(dnu)/dx`
Hence, Eq.(1) can be written as
`nu (dnu)/dx=-ω^2x`
`∴ nudnu=- ω^2 xdx`
Integrating this expression, we get
`nu^2/2 = (-ω ^2x^2)/2+c`
where the constant of integration C is found from a boundary condition.
At an extreme position (a turning point of the motion), the velocity of the particle is zero. Thus, ν = 0 when `x = +- A`, where A is the amplitude.
∴ `0= (-ω^2A^2)/2+C` ` ∴ C = (ω^2 A^2)/2`
∴ `nu^2 /2 = (-ω^2x^2)/2 + (ω^2A^2)/2`
∴ `nu^2 =ω^2 (A^2 -x^2) `
∴ `nu= +- ω sqrt (A^2-X^2)`
This euation gives the velocity of the particle in terms of the displacement, x. The velocity towards right is taken to be positive and toward left as negative. Since, `nu = dx//dt` we can write Eq. (2) as follows :
`dx/dt =ω sqrt(A^2-X^2)`
∴ `dx/sqrt (A^2-X^2)=ω\ dt `
Integrating this expression, we get,
`sin^-1 (x/A)=ωt+ alpha`...................(3)
where the constant of integration, `alpha `, is found from the initial conditions, i.e., the displacement and the velocity of the particle at time t = 0
From equation (3), we have
`x/A= sin (ωt+alpha)`
∴ Displacement as a function of time is,
`x = A sin (ωt + alpha)`
APPEARS IN
RELATED QUESTIONS
A particle performing linear S.H.M. has a period of 6.28 seconds and a pathlength of 20 cm. What is the velocity when its displacement is 6 cm from mean position?
Define linear S.H.M.
The maximum velocity of a particle performing linear S.H.M. is 0.16 m/s. If its maximum acceleration is 0.64 m/s2, calculate its period.
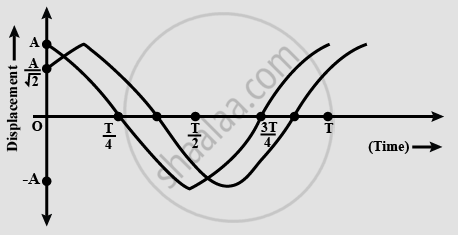
Two particles perform linear simple harmonic motion along the same path of length 2A and period T as shown in the graph below. The phase difference between them is ___________.
Obtain the differential equation of linear simple harmonic motion.
A particle executing linear S.H.M. has velocities v1 and v2 at distances x1 and x2 respectively from the mean position. The angular velocity of the particle is _______
A particle performing linear S.H.M. has the maximum velocity of 25 cm/s and maximum acceleration of 100 cm/ m2. Find the amplitude and period of oscillation. (π = 3.142)
In SI units, the differential equation of an S.H.M. is `("d"^2"x")/("dt"^2)` = − 36x. Find its frequency and period.
A body of mass m performs linear S.H.M. given by equation, x = P sin cot + Q sin`(omega"t" + pi/2)`. The total energy of the particle at any instant is ______.
A particle performing Linear S.H.M. has a maximum velocity 25 cm/sand maximum acceleration 100 cm/s2. Find the period of oscillations.
What is the rotational analogue of Newton's second law of motion?
The speeds of a particle performing linear SHM are 8 units and 6 units at respective displacements of 6 cm and 8 cm. Find its period and amplitude.
A spring balance has a scale that reads from 0 to 50 kg. The length of the scale is 20 cm. A body suspended from this balance, when displaced and released osillates with a period of 0.6 sec. What is the weight of the body?
