Advertisements
Advertisements
Question
How will you represent first order reactions graphically.
Solution
i. The differential rate law for the first-order reaction A → P is 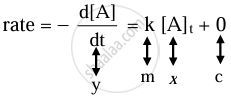
The equation is of the form y = mx + c. A plot of rate versus [A]t is a straight line passing through the origin. The slope of straight line = k.
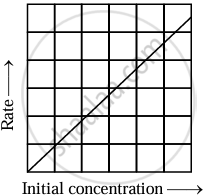 |
| Variation of rate with [A] |
ii. The integrated rate law is
k = `2.303/t log_10 ["A"]_0/["A"]_"t"`
On rearrangement, the equation becomes
`(kt)/2.303 = log_10 ["A"]_0 - log_10 ["A"]_"t"`
Hence,
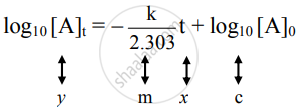
The equation is of the straight line. A graph of `log_10[A]_t` versus t yields a straight line with slope `-"k"/2.303` and y-axis intercepts as log10[A]0.
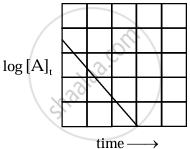 |
| Variation of `log_10 [A]_t` with time |
iii. Rearranging the integrated rate law equation, we get
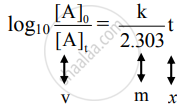
The equation has a straight-line form y = mx. Hence, the graph of `log_10 ([A]_0)/([A]_t)` versus t is a straight line passing through the origin.
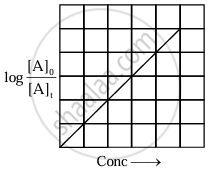 |
| Variation of `log_10 ([A]_0)/([A]_t)` with time |
APPEARS IN
RELATED QUESTIONS
Answer the following in one or two sentences.
Write the relationships between rate constant and half-life of the first order and zeroth-order reactions.
Solve
In a first-order reaction, the concentration of the reactant decreases from 20 mmol dm-3 to 8 mmol dm-3 in 38 minutes. What is the half-life of reaction?
Solve
The half-life of a first-order reaction is 1.7 hours. How long will it take for 20% of the reactant to react?
For first order reaction, the rate constant for the decomposition of N2O5 is 6 × 10–4 s –1. The half-life period for decomposition in seconds is ______.
Write a mathematical expression for integrated rate law for zero-order reaction.
Derive an expression for the relation between half-life and rate constant for first-order reaction.
For a first order reaction \[\ce{A ->Product}\] with initial concentration x mol L−1, has a half life period of 2.5 hours. For the same reaction with initial concentration `("x"/2)` mol L−1 the half life is
Assertion: rate of reaction doubles when the concentration of the reactant is doubles if it is a first-order reaction.
Reason: rate constant also doubles.
Write the rate law for the following reaction.
A reaction that is `3/2` order in x and zero order in y.
A zero order reaction is 20% complete in 20 minutes. Calculate the value of the rate constant. In what time will the reaction be 80% complete?
From the following data, show that the decomposition of hydrogen peroxide is a reaction of the first order:
| t (min) | 0 | 10 | 20 |
| V (ml) | 46.1 | 29.8 | 19.3 |
Where t is the time in minutes and V is the volume of standard KMnO4 solution required for titrating the same volume of the reaction mixture.
The rate of the reaction \[\ce{A + B -> C}\] is 3.6 × 10−2 mol dm−3 s−1 when [A] = 0.3 mol dm−3 and [B] = 0.2 mol dm−3. Calculate k if reaction is first order in A and zero order in B.
A first order reaction has rate constant 1 × 10−2 s−1. What time will, it take for 20 g or reactant to reduce to 5 g?
Which among the following reaction is an example of a zero order reaction?
If [A] is the concentration of A at any time t and [A]0 is the concentration at t = 0, then for the 1st order reaction, the rate equation can be written as ____________.
If [A]0 is the initial concentration, then the half life of zero order reaction is ____________.
In a first order reaction, the concentration of the reactant, decreases from 0.8 mol dm−3 to 0.4 mol dm−3 in 15 minutes. The time taken for the concentration to change from 0.1 mol dm−3 to 0.025 mol dm−3 is ____________.
The integrated rate equation for first-order reaction, A → product, is ______.
The slope of a graph, log [A]t versus 't' for a first order reaction is −2.5 × 10−3 s−1. The rate constant for the reaction is ____________.
The initial concentration of reactant (A) is 2 mol dm−3 for a zero order reaction \[\ce{A -> B}\]. The rate constant (k) is related to its half-life `("t"_(1//2))` by the equation:
Which among the following is an example of pseudo first order reaction?
In a reaction \[\ce{N2_{(g)} + 3H2_{(g)} -> 2NH3_{(g)}}\], if the rate of disappearance of N2(g) is 2.6 × 10−4 M/s, the rate of disappearance of H2(g) in M/s is ____________.
Half-life of first-order reaction \[\ce{X -> Y + Z}\] is 3 minutes. What is the time required to reduce the concentration of 'X' by 90 % of it's initial concentration?
For zero order reaction, when [A]t is plotted against time (t), the slope of the straight line obtained is equal to ______.
The rate constant for a first order reaction is 7.0 × 10-4 s-1. If initial concentration of reactant is 0.080 M, what is the half-life of reaction?
Calculate half-life of a first order reaction in minute if the rate constant is 1 × 10-3 s-1.
Which is the relation between half life and rate constant for a zero order?
