Advertisements
Advertisements
Question
If a : b : : c : d, then prove that
2a+7b : 2a-7b = 2c+7d : 2c-7d
Solution
2a+7b : 2a-7b = 2c+7d : 2c -7d
`"a"/"b" = "c"/"d"`
Multiplying both sides by `2/7`
`=> "a"/"b" xx 2/7 = "c"/"d" xx 2/7`
`=> (2"a")/(7"b") = (2"c")/(7"d")`
Applying componendo and dividendo,
`(2"a" + 7"b")/(2"a" - 7"b") = (2"c" + 7"d")/(2"c" - 7"d")`
Hence, 2a+7b : 2a-7b = 2c+7d : 2c-7d
APPEARS IN
RELATED QUESTIONS
If three quantities are in continued proportion; show that the ratio of the first to the third is the duplicate ratio of the first to the second.
If `x/a = y/b = z/c` prove that `(2x^3 - 3y^3 + 4z^3)/(2a^3 - 3b^3 + 4c^3) = ((2x - 3y + 4z)/(2a - 3b + 4c))^3`
Find the two numbers such that their mean proprtional is 24 and the third proportinal is 1,536.
If b is the mean proportional between a and c, prove that `(a^2 - b^2 + c^2)/(a^-2 -b^-2 + c^-2)` = b4.
If `x/a = y/b = z/c`, prove that `x^3/a^2 + y^2/b^2 + z^3/c^2 = ((x + y + z)^3)/((a + b ++ c)^2)`.
Determine if the following ratio form a proportion:
25 cm : 1 m and Rs 40 : Rs 160
7 Persons is to 49 Persons as 11 kg is to 88 kg
10 books is to 15 books as 3 books is to 15 books
Sleeping time of a python in a 24 hour clock is represented by the shaded portion in figure.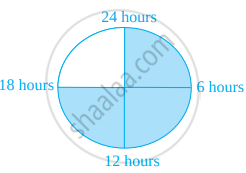
The ratio of sleeping time to awaking time is ______.
If `(a + b)^3/(a - b)^3 = 64/27`.
- Find `(a + b)/(a - b)`
- Hence using properties of proportion, find a : b.
