Advertisements
Advertisements
Question
If fourth degree polynomial is divided by a quadratic polynomial, write the degree of the remainder.
Solution
Here `f (x)` represent dividend and g(x) represent divisor.
`g (x)` =quadratic polynomial
`g(x)= ax^2 + bx + c`
Therefore degree of `(f(x))=4`
Degree of `(g(x))= 2`
The quotient q(x) is of degree `2 (=4-2)`
The remainder `r (x)` is of degree 1 or less.
Hence, the degree of the remainder is equal to 1 or less than 1
APPEARS IN
RELATED QUESTIONS
In Q. No. 15, write the sign of c.
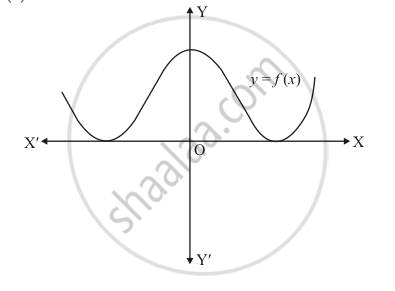
The graph of a polynomial f(x) is as shown in Fig. 2.21. Write the number of real zeros of f(x).
If f(x) = x3 + x2 − ax + b is divisible by x2 − x write the value of a and b.
If 1 is a zero of the polynomial p(x) = ax2 − 3(a − 1) x − 1, then find the value of a.
Divide. Write the quotient and the remainder.
40m5 ÷ 30m3
Divide. Write the quotient and the remainder.
(2y3 + 4y2 + 3) ÷ 2y2
Given that two of the zeroes of the cubic poly-nomial ax3 + bx2 + cx + d are 0, the third zero is ______.
Determine the degree of the following polynomial:
–10
For the polynomial `((x^3 + 2x + 1))/5 - 7/2 x^2 - x^6`, write the coefficient of x3
Classify the following as a constant, linear, quadratic and cubic polynomials:
3
