Advertisements
Advertisements
Question
If points A, B and C have position vectors `2hati, hatj` and `2hatk` respectively, then show that ΔABC is an isosceles triangle.
Solution
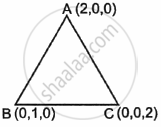
Using distance formula
AB = `sqrt((0 - 2)^2 + (1 - 0)^2 + (0 - 0)^2`
= `sqrt(4 + 1)`
AB = `sqrt(5)` units
BC = `sqrt((0 - 0)^2 + (0 - 1)^2 + (2 - 0)^2`
= `sqrt(1 + 4)`
= `sqrt(5)`
BC = `sqrt(5)` units
AC = `sqrt((0 - 2)^2 + (0 - 0)^2 + (2 - 0)^2`
= `sqrt(4 + 4)`
= `2sqrt(2)`
∵ AB = BC = `sqrt(5) ≠ AC`
`\implies` ΔABC is an isosceles triangle.
APPEARS IN
RELATED QUESTIONS
Find the direction ratios of a vector perpendicular to the two lines whose direction ratios are -2, 1, -1, and -3, -4, 1.
Find the value of 'p' for which the vectors `3hati+2hatj+9hatk and hati-2phatj+3hatk` are parallel
Represent graphically a displacement of 40 km, 30° east of north.
Classify the following as scalar and vector quantity.
Time period
In Figure, identify the following vector.

Coinitial
Find the direction cosines of the vector `hati + 2hatj + 3hatk`.
Find the direction cosines of the vector joining the points A (1, 2, -3) and B (-1, -2, 1) directed from A to B.
Show that the vector `hati + hatj + hatk` is equally inclined to the axes OX, OY, and OZ.
Find the position vector of the mid point of the vector joining the points P (2, 3, 4) and Q (4, 1, – 2).
Write down a unit vector in XY-plane, making an angle of 30° with the positive direction of the x-axis.
If θ is the angle between two vectors `veca` and `vecb`, then `veca . vecb >= 0` only when ______.
Express \[\vec{AB}\] in terms of unit vectors \[\hat{i}\] and \[\hat{j}\], when the points are A (4, −1), B (1, 3)
Find \[\left| \vec{A} B \right|\] in each case.
Express \[\vec{AB}\] in terms of unit vectors \[\hat{i}\] and \[\hat{j}\], when the points are A (−6, 3), B (−2, −5)
Find \[\left| \vec{A} B \right|\] in each case.
Find the angle between the vectors \[\vec{a} \text{ and } \vec{b}\] \[\vec{a} = 3\hat{i} - 2\hat{j} - 6\hat{k} \text{ and } \vec{b} = 4 \hat{i} - \hat{j} + 8 \hat{k}\]
Find the angle between the vectors \[\vec{a} \text{ and } \vec{b}\] \[\vec{a} = 2\hat{i} - \hat{j} + 2\hat{k} \text{ and } \vec{b} = 4\hat{i} + 4 \hat{j} - 2\hat{k}\]
The adjacent sides of a parallelogram are represented by the vectors \[\vec{a} = \hat{i} + \hat{j} - \hat{k}\text{ and }\vec{b} = - 2 \hat{i} + \hat{j} + 2 \hat{k} .\]
Find unit vectors parallel to the diagonals of the parallelogram.
Dot products of a vector with vectors \[\hat{i} - \hat{j} + \hat{k} , 2\hat{ i} + \hat{j} - 3\hat{k} \text{ and } \text{i} + \hat{j} + \hat{k}\] are respectively 4, 0 and 2. Find the vector.
If \[\vec{a,} \vec{b,} \vec{c}\] are three mutually perpendicular unit vectors, then prove that \[\left| \vec{a} + \vec{b} + \vec{c} \right| = \sqrt{3}\]
For any two vectors \[\vec{a} \text{ and } \vec{b}\] show that \[\left( \vec{a} + \vec{b} \right) \cdot \left( \vec{a} - \vec{b} \right) = 0 \Leftrightarrow \left| \vec{a} \right| = \left| \vec{b} \right|\]
If \[\vec{a} = 2 \hat{i} - \hat{j} + \hat{k}\] \[\vec{b} = \hat{i} + \hat{j} - 2 \hat{k}\] \[\vec{c} = \hat{i} + 3 \hat{j} - \hat{k}\] find λ such that \[\vec{a}\] is perpendicular to \[\lambda \vec{b} + \vec{c}\]
If \[\vec{p} = 5 \hat{i} + \lambda \hat{j} - 3 \hat{k} \text{ and } \vec{q} = \hat{i} + 3 \hat{j} - 5 \hat{k} ,\] then find the value of λ, so that \[\vec{p} + \vec{q}\] and \[\vec{p} - \vec{q}\] are perpendicular vectors.
Show that the vectors \[\vec{a} = 3 \hat{i} - 2 \hat{j} + \hat{k} , \vec{b} = \hat{i} - 3 \hat{j} + 5 \hat{k} , \vec{c} = 2 \hat{i} + \hat{j} - 4 \hat{k}\] form a right-angled triangle.
Find the magnitude of two vectors \[\vec{a} \text{ and } \vec{b}\] that are of the same magnitude, are inclined at 60° and whose scalar product is 1/2.
If the vertices A, B and C of ∆ABC have position vectors (1, 2, 3), (−1, 0, 0) and (0, 1, 2), respectively, what is the magnitude of ∠ABC?
Find the value of x for which \[x \left( \hat{i} + \hat{j} + \hat{k} \right)\] is a unit vector.
Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are `hati + 2hatj - hatk` and `-hati + hatj + hatk` respectively, internally the ratio 2:1.
