Advertisements
Advertisements
Question
The adjacent sides of a parallelogram are represented by the vectors \[\vec{a} = \hat{i} + \hat{j} - \hat{k}\text{ and }\vec{b} = - 2 \hat{i} + \hat{j} + 2 \hat{k} .\]
Find unit vectors parallel to the diagonals of the parallelogram.
Solution
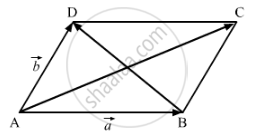
\[\vec{a} = \hat{i} + \hat{j} - \hat{k} \text{ and }\vec{b} = - 2 \hat{i} + \hat{j} + 2 \hat{k} .\]
\[\overrightarrow{AC} = \vec{a} + \vec{b} = - \hat{i} + 2 \hat{j} + \hat{k}\]
\[\text{Let the unit vector along the diagonals AC and BD of the parallelogram be }\widehat{AC}\text{ and }\widehat{BD} . \]
\[ \Rightarrow \widehat{AC} = \frac{- \hat{i} + 2 \hat{j} + \hat{k}}{\sqrt{6}}\]
\[\Rightarrow \widehat{BD} = \frac{- 3 \hat{i} + 3 \hat{k}}{3\sqrt{2}} = \frac{- \hat{i} + k}{\sqrt{2}}\]
APPEARS IN
RELATED QUESTIONS
If `bara, barb, bar c` are the position vectors of the points A, B, C respectively and ` 2bara + 3barb - 5barc = 0` , then find the ratio in which the point C divides line segment AB.
Write the position vector of the point which divides the join of points with position vectors `3veca-2vecb and 2veca+3vecb` in the ratio 2 : 1.
Find the position vector of the foot of perpendicular and the perpendicular distance from the point P with position vector
`2hati+3hatj+4hatk` to the plane `vecr` . `(2hati+hatj+3hatk)−26=0` . Also find image of P in the plane.
Represent graphically a displacement of 40 km, 30° east of north.
In Figure, identify the following vector.

Coinitial
`veca and -veca` are collinear.
Two collinear vectors are always equal in magnitude.
Two collinear vectors having the same magnitude are equal.
Find the direction cosines of the vector `hati + 2hatj + 3hatk`.
Find the direction cosines of the vector joining the points A (1, 2, -3) and B (-1, -2, 1) directed from A to B.
Find the position vector of the mid point of the vector joining the points P (2, 3, 4) and Q (4, 1, – 2).
Write down a unit vector in XY-plane, making an angle of 30° with the positive direction of the x-axis.
If θ is the angle between two vectors `veca` and `vecb`, then `veca . vecb >= 0` only when ______.
Express \[\vec{AB}\] in terms of unit vectors \[\hat{i}\] and \[\hat{j}\], when the points are A (4, −1), B (1, 3)
Find \[\left| \vec{A} B \right|\] in each case.
Find the angle between the vectors \[\vec{a} \text{ and } \vec{b}\] \[\vec{a} = 2\hat{i} - \hat{j} + 2\hat{k} \text{ and } \vec{b} = 4\hat{i} + 4 \hat{j} - 2\hat{k}\]
Find a unit vector parallel to the vector \[\hat{i} + \sqrt{3} \hat{j}\]
Find the angle between the vectors \[\vec{a} = 2 \hat{i} - 3 \hat{j} + \hat{k} \text{ and } \vec{b} = \hat{i} + \hat{j} - 2 \hat{k}\]
Find the angles which the vector \[\vec{a} = \hat{i} -\hat {j} + \sqrt{2} \hat{k}\] makes with the coordinate axes.
Dot product of a vector with \[\hat{i} + \hat{j} - 3\hat{k} , \hat{i} + 3\hat{j} - 2 \hat{k} \text{ and } 2 \hat{i} + \hat{j} + 4 \hat{k}\] are 0, 5 and 8 respectively. Find the vector.
Dot products of a vector with vectors \[\hat{i} - \hat{j} + \hat{k} , 2\hat{ i} + \hat{j} - 3\hat{k} \text{ and } \text{i} + \hat{j} + \hat{k}\] are respectively 4, 0 and 2. Find the vector.
If \[\hat{ a } \text{ and } \hat{b }\] are unit vectors inclined at an angle θ, prove that
\[\tan\frac{\theta}{2} = \frac{\left| \hat{a} -\hat{b} \right|}{\left| \hat{a} + \hat{b} \right|}\]
If \[\vec{p} = 5 \hat{i} + \lambda \hat{j} - 3 \hat{k} \text{ and } \vec{q} = \hat{i} + 3 \hat{j} - 5 \hat{k} ,\] then find the value of λ, so that \[\vec{p} + \vec{q}\] and \[\vec{p} - \vec{q}\] are perpendicular vectors.
If either \[\vec{a} = \vec{0} \text{ or } \vec{b} = \vec{0}\] then \[\vec{a} \cdot \vec{b} = 0 .\] But the converse need not be true. Justify your answer with an example.
Find the unit vector in the direction of vector \[\overrightarrow{PQ} ,\]
where P and Q are the points (1, 2, 3) and (4, 5, 6).
If \[\vec{a} = \hat{i} + \hat{j} + \hat{k} , \vec{b} = 2 \hat{i} - \hat{j} + 3 \hat{k} \text{ and }\vec{c} = \hat{i} - 2 \hat{j} + \hat{k} ,\] find a unit vector parallel to \[2 \vec{a} - \vec{b} + 3 \vec{c .}\]
If \[\vec{a} \times \vec{b} = \vec{c} \times \vec{d} \text { and } \vec{a} \times \vec{c} = \vec{b} \times \vec{d}\] , show that \[\vec{a} - \vec{d}\] is parallel to \[\vec{b} - \vec{c}\] where \[\vec{a} \neq \vec{d} \text { and } \vec{b} \neq \vec{c}\] .
if `hat"i" + hat"j" + hat"k", 2hat"i" + 5hat"j", 3hat"i" + 2 hat"j" - 3hat"k" and hat"i" - 6hat"j" - hat"k"` respectively are the position vectors A, B, C and D, then find the angle between the straight lines AB and CD. Find whether `vec"AB" and vec"CD"` are collinear or not.
A vector `vec"r"` has magnitude 14 and direction ratios 2, 3, – 6. Find the direction cosines and components of `vec"r"`, given that `vec"r"` makes an acute angle with x-axis.
Find the sine of the angle between the vectors `vec"a" = 3hat"i" + hat"j" + 2hat"k"` and `vec"b" = 2hat"i" - 2hat"j" + 4hat"k"`.
If A, B, C, D are the points with position vectors `hat"i" + hat"j" - hat"k", 2hat"i" - hat"j" + 3hat"k", 2hat"i" - 3hat"k", 3hat"i" - 2hat"j" + hat"k"`, respectively, find the projection of `vec"AB"` along `vec"CD"`.
Let (h, k) be a fixed point where h > 0, k > 0. A straight line passing through this point cuts the positive direction of the coordinate axes at the points P and Q. Then the minimum area of the ΔOPQ. O being the origin, is
If points A, B and C have position vectors `2hati, hatj` and `2hatk` respectively, then show that ΔABC is an isosceles triangle.
