Advertisements
Advertisements
प्रश्न
The adjacent sides of a parallelogram are represented by the vectors \[\vec{a} = \hat{i} + \hat{j} - \hat{k}\text{ and }\vec{b} = - 2 \hat{i} + \hat{j} + 2 \hat{k} .\]
Find unit vectors parallel to the diagonals of the parallelogram.
उत्तर
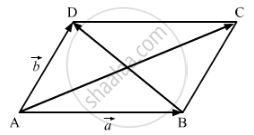
\[\vec{a} = \hat{i} + \hat{j} - \hat{k} \text{ and }\vec{b} = - 2 \hat{i} + \hat{j} + 2 \hat{k} .\]
\[\overrightarrow{AC} = \vec{a} + \vec{b} = - \hat{i} + 2 \hat{j} + \hat{k}\]
\[\text{Let the unit vector along the diagonals AC and BD of the parallelogram be }\widehat{AC}\text{ and }\widehat{BD} . \]
\[ \Rightarrow \widehat{AC} = \frac{- \hat{i} + 2 \hat{j} + \hat{k}}{\sqrt{6}}\]
\[\Rightarrow \widehat{BD} = \frac{- 3 \hat{i} + 3 \hat{k}}{3\sqrt{2}} = \frac{- \hat{i} + k}{\sqrt{2}}\]
APPEARS IN
संबंधित प्रश्न
Find the position vector of the foot of perpendicular and the perpendicular distance from the point P with position vector
`2hati+3hatj+4hatk` to the plane `vecr` . `(2hati+hatj+3hatk)−26=0` . Also find image of P in the plane.
If `bara, barb, barc` are position vectors of the points A, B, C respectively such that `3bara+ 5barb-8barc = 0`, find the ratio in which A divides BC.
Represent graphically a displacement of 40 km, 30° east of north.
In Figure, identify the following vector.

Coinitial
`veca and -veca` are collinear.
Two collinear vectors are always equal in magnitude.
Two vectors having the same magnitude are collinear.
Find the direction cosines of the vector `hati + 2hatj + 3hatk`.
Find the direction cosines of the vector joining the points A (1, 2, -3) and B (-1, -2, 1) directed from A to B.
Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are `hati + 2hatj - hatk` and `-hati + hatj + hatk` respectively, externally in the ratio 2:1.
Find the position vector of the mid point of the vector joining the points P (2, 3, 4) and Q (4, 1, – 2).
Show that the points A, B and C with position vectors `veca = 3hati - 4hatj - 4hatk`, `vecb = 2hati - hatj + hatk` and `vecc = hati - 3hatj - 5hatk`, respectively form the vertices of a right angled triangle.
Let `veca` and `vecb` be two unit vectors, and θ is the angle between them. Then `veca + vecb` is a unit vector if ______.
Find a vector of magnitude 4 units which is parallel to the vector \[\sqrt{3} \hat{i} + \hat{j}\]
Express \[\vec{AB}\] in terms of unit vectors \[\hat{i}\] and \[\hat{j}\], when the points are A (−6, 3), B (−2, −5)
Find \[\left| \vec{A} B \right|\] in each case.
Find the angle between the vectors \[\vec{a} = 2 \hat{i} - 3 \hat{j} + \hat{k} \text{ and } \vec{b} = \hat{i} + \hat{j} - 2 \hat{k}\]
Find the angles which the vector \[\vec{a} = \hat{i} -\hat {j} + \sqrt{2} \hat{k}\] makes with the coordinate axes.
If \[\hat{ a } \text{ and } \hat{b }\] are unit vectors inclined at an angle θ, prove that
\[\tan\frac{\theta}{2} = \frac{\left| \hat{a} -\hat{b} \right|}{\left| \hat{a} + \hat{b} \right|}\]
For any two vectors \[\vec{a} \text{ and } \vec{b}\] show that \[\left( \vec{a} + \vec{b} \right) \cdot \left( \vec{a} - \vec{b} \right) = 0 \Leftrightarrow \left| \vec{a} \right| = \left| \vec{b} \right|\]
If \[\vec{a} = 2 \hat{i} - \hat{j} + \hat{k}\] \[\vec{b} = \hat{i} + \hat{j} - 2 \hat{k}\] \[\vec{c} = \hat{i} + 3 \hat{j} - \hat{k}\] find λ such that \[\vec{a}\] is perpendicular to \[\lambda \vec{b} + \vec{c}\]
If \[\vec{\alpha} = 3 \hat{i} + 4 \hat{j} + 5 \hat{k} \text{ and } \vec{\beta} = 2 \hat{i} + \hat{j} - 4 \hat{k} ,\] then express \[\vec{\beta}\] in the form of \[\vec{\beta} = \vec{\beta_1} + \vec{\beta_2} ,\] where \[\vec{\beta_1}\] is parallel to \[\vec{\alpha} \text{ and } \vec{\beta_2}\] is perpendicular to \[\vec{\alpha}\]
If either \[\vec{a} = \vec{0} \text{ or } \vec{b} = \vec{0}\] then \[\vec{a} \cdot \vec{b} = 0 .\] But the converse need not be true. Justify your answer with an example.
If \[\vec{a} = 2 \hat{i} + 2 \hat{j} + 3 \hat{k} , \vec{b} = - \hat{i} + 2 \hat{j} + \hat{k} \text{ and } \vec{c} = 3 \hat{i} + \hat{j}\] \[\vec{a} + \lambda \vec{b}\] is perpendicular to \[\vec{c}\] then find the value of λ.
If the vertices A, B and C of ∆ABC have position vectors (1, 2, 3), (−1, 0, 0) and (0, 1, 2), respectively, what is the magnitude of ∠ABC?
Find the unit vector in the direction of vector \[\overrightarrow{PQ} ,\]
where P and Q are the points (1, 2, 3) and (4, 5, 6).
If \[\vec{a} = \hat{i} + \hat{j} + \hat{k} , \vec{b} = 2 \hat{i} - \hat{j} + 3 \hat{k} \text{ and }\vec{c} = \hat{i} - 2 \hat{j} + \hat{k} ,\] find a unit vector parallel to \[2 \vec{a} - \vec{b} + 3 \vec{c .}\]
Show that the vectors \[2 \hat{i} - 3 \hat{j} + 4 \hat{k}\text{ and }- 4 \hat{i} + 6 \hat{j} - 8 \hat{k}\] are collinear.
A vector `vec"r"` has magnitude 14 and direction ratios 2, 3, – 6. Find the direction cosines and components of `vec"r"`, given that `vec"r"` makes an acute angle with x-axis.
Position vector of a point P is a vector whose initial point is origin.
Let (h, k) be a fixed point where h > 0, k > 0. A straight line passing through this point cuts the positive direction of the coordinate axes at the points P and Q. Then the minimum area of the ΔOPQ. O being the origin, is
Area of rectangle having vertices A, B, C and D will position vector `(- hati + 1/2hatj + 4hatk), (hati + 1/2hatj + 4hatk) (hati - 1/2hatj + 4hatk)` and `(-hati - 1/2hatj + 4hatk)` is
Assertion (A): If a line makes angles α, β, γ with positive direction of the coordinate axes, then sin2 α + sin2 β + sin2 γ = 2.
Reason (R): The sum of squares of the direction cosines of a line is 1.
A line l passes through point (– 1, 3, – 2) and is perpendicular to both the lines `x/1 = y/2 = z/3` and `(x + 2)/-3 = (y - 1)/2 = (z + 1)/5`. Find the vector equation of the line l. Hence, obtain its distance from the origin.
If points A, B and C have position vectors `2hati, hatj` and `2hatk` respectively, then show that ΔABC is an isosceles triangle.
