Advertisements
Advertisements
Question
If the bar magnet is turned around by 180°, where will the new null points be located?
Solution
The magnetic field on the axis of the magnet at a distance d1 = 14 cm, can be written as:
`"B"_1 = (μ_0 2"M")/(4pi ("d"_1)^3) = "H"` .......(1)
Where,
M = Magnetic moment
μ0 = Permeability of free space
H = Horizontal component of the magnetic field at d1
If the bar magnet is turned through 180°, then the neutral point will lie on the equatorial line.
Hence, the magnetic field at a distance d2, on the equatorial line of the magnet can be written as:
`"B"_2 = (μ_0 "M")/(4pi ("d"_2)^3) = "H"` .............(2)
Equating equations (1) and (2), we get:
`2/("d"_1)^3 = 1/("d"_2)^3`
`("d"_2/"d"_1)^3 = 1/2`
∴ `"d"_2 = "d"_1 xx (1/2)^(1/3)`
= 14 × 0.794
= 11.1 cm
The new null points will be located 11.1 cm on the normal bisector.
APPEARS IN
RELATED QUESTIONS
Magnetic lines of force are closed continuous curves.
A bar magnet of length 1 cm and cross-sectional area 1.0 cm2 produces a magnetic field of 1.5 × 10−4 T at a point in end-on position at a distance 15 cm away from the centre. (a) Find the magnetic moment M of the magnet. (b) Find the magnetisation I of the magnet. (c) Find the magnetic field B at the centre of the magnet.
Answer the following question.
Write the four important properties of the magnetic field lines due to a bar magnet.
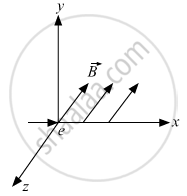
An electron moves along +x direction. It enters into a region of uniform magnetic field. `vecB` directed along –z direction as shown in fig. Draw the shape of the trajectory followed by the electron after entering the field.
Choose the correct option.
Inside a bar magnet, the magnetic field lines
Answer the following question in detail.
A circular magnet is made with its north pole at the centre, separated from the surrounding circular south pole by an air gap. Draw the magnetic field lines in the gap.
Answer the following question in detail.
Two bar magnets are placed on a horizontal surface. Draw magnetic lines around them. Mark the position of any neutral points (points where there is no resultant magnetic field) on your diagram.
A short bar magnet placed with its axis at 30° with a uniform external magnetic field of 0.25 T experiences a torque of magnitude equal to 4.5 × 10–2 J. What is the magnitude of magnetic moment of the magnet?
A closely wound solenoid of 2000 turns and area of cross-section 1.6 × 10-4 m2 , carrying a current of 4.0 A, is suspended through its centre allowing it to turn in a horizontal plane.
What is the force and torque on the solenoid if a uniform horizontal magnetic field of 7.5 × 10-2 T is set up at an angle of 30° with the axis of the solenoid?
Magnetic field at far axial point due to solenoid as well as bar magnet varies ______.
According to the dipole analogy 1/ε0 corresponds to ______.
When a current is passed through a tangent galvanometer, it gives a deflection of 30° for 60° correction, the current must be
A bar magnet of magnetic moment 3.0 Am is placed in a uniform magnetic field of 2 × 10-5T. If each pole of the magnet experience a force of 6 × 10-4 N, the length of the magnet is ______.
A proton has spin and magnetic moment just like an electron. Why then its effect is neglected in magnetism of materials?
Suppose we want to verify the analogy between electrostatic and magnetostatic by an explicit experiment. Consider the motion of (i) electric dipole p in an electrostatic field E and (ii) magnetic dipole m in a magnetic field B. Write down a set of conditions on E, B, p, m so that the two motions are verified to be identical. (Assume identical initial conditions.)
Use (i) the Ampere’s law for H and (ii) continuity of lines of B, to conclude that inside a bar magnet, (a) lines of H run from the N pole to S pole, while (b) lines of B must run from the S pole to N pole.
A long straight wire of circular cross section of radius 'a' carries a steady current I. The current is uniformly distributed across its cross section. The ratio of magnitudes of the magnetic field at a point `a/2` above the surface of wire to that of a point `a/2` below its surface is ______.
