Advertisements
Advertisements
Question
In a parallelogram ABCD, ∠B = 105°. Determine the measure of ∠A and ∠D.
Solution
Given: ∠B = 105°.
We know that the sum of any two successive parallelogram angles is 180°.
∴ ∠A + ∠B = 180°
⇒ ∠A + 105° = 180°
⇒ ∠A = 180° – 105°
= 75°
Also, ∠A + ∠D = 180°
⇒ 75 + ∠D = 180°
⇒ ∠D = 180° – 75°
= 105°
Hence, ∠A = 75° and ∠D = 105°.
APPEARS IN
RELATED QUESTIONS
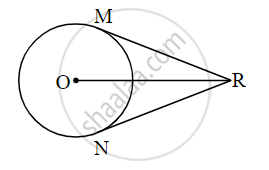
In the adjoining figure, O is the centre of the circle. From point R, seg RM and seg RN are tangent segments touching the circle at M and N. If (OR) = 10 cm and radius of the circle = 5 cm, then
- What is the length of each tangent segment?
- What is the measure of ∠MRO?
- What is the measure of ∠MRN?

Seg RM and seg RN are tangent segments of a circle with centre O. Prove that seg OR bisects ∠MRN as well as ∠MON with the help of activity.
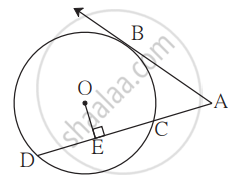
In the given figure, O is the centre of the circle and B is a point of contact. seg OE ⊥ seg AD, AB = 12, AC = 8, find (1) AD (2) DC (3) DE.
In the given figure, seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE × GE = 4r2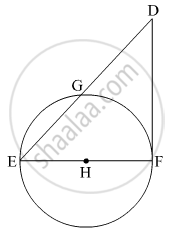
Four alternative answers for the following question is given. Choose the correct alternative.
Length of a tangent segment drawn from a point which is at a distance 12.5 cm from the centre of a circle is 12 cm, find the diameter of the circle.
The perpendicular height of a cone is 12 cm and its slant height is 13 cm. Find the radius of the base of the cone.
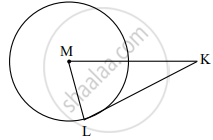
In the given figure, M is the centre of the circle and seg KL is a tangent segment. L is a point of contact. If MK = 12, KL = `6sqrt3`, then find the radius of the circle.
Prove the following theorem:
Tangent segments drawn from an external point to the circle are congruent.
Segment DP and segment DQ are tangent segments to the circle with center A. If DP = 7 cm. So find the length of the segment DQ.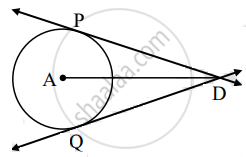
The chords corresponding to congruent arcs of a circle are congruent. Prove the theorem by completing following activity.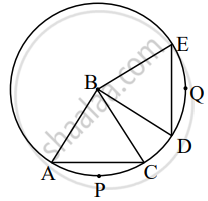
Given: In a circle with centre B
arc APC ≅ arc DQE
To Prove: Chord AC ≅ chord DE
Proof: In ΔABC and ΔDBE,
side AB ≅ side DB ......`square`
side BC ≅ side `square` .....`square`
∠ABC ≅ ∠DBE ......[Measure of congruent arcs]
∆ABC ≅ ∆DBE ......`square`
In the adjoining figure, O is the center of the circle. From point R, seg RM and seg RN are tangent segments touching the circle at M and N. If (OR) = 10 cm and radius of the circle = 5 cm, then
(i) What is the length of each tangent segment?
(ii) What is the measure of ∠MRO?
(iii) What is the measure of ∠MRN?
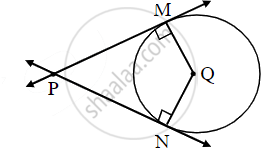
In the adjoining figure circle with Centre, Q touches the sides of ∠MPN at M and N. If ∠MPN = 40°, find measure of ∠MQN.
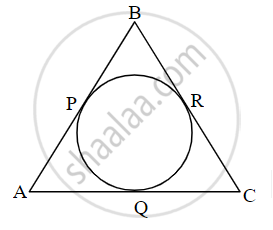
The figure ΔABC is an isosceles triangle with a perimeter of 44 cm. The sides AB and BC are congruent and the length of the base AC is 12 cm. If a circle touches all three sides as shown in the figure, then find the length of the tangent segment drawn to the circle from point B.
If AB and CD are the common tangents in the circles of two unequal (different) radii, then show that seg AB ≅ seg CD.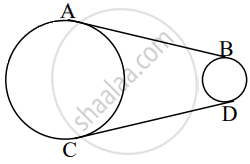
Seg RM and seg RN are tangent segments of a circle with centre O. Prove that seg OR bisects ∠MRN as well as ∠MON with the help of activity.

Proof: In ∆RMO and ∆RNO,
∠RMO ≅ ∠RNO = 90° ......[`square`]
hypt OR ≅ hypt OR ......[`square`]
seg OM ≅ seg `square` ......[Radii of the same circle]
∴ ∆RMO ≅ ∆RNO ......[`square`]
∠MOR ≅ ∠NOR
Similairy ∠MRO ≅ `square` ......[`square`]
