Advertisements
Advertisements
Question
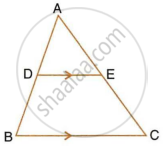
In ΔABC, DE is parallel to BC and DE = 3:8.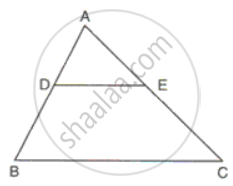
Find:
(i) AD : BD
(ii) AE, if AC = 16.
Solution
(i) Since DE ||BC
`"DE"/"BC" = "AD"/"AB"`
⇒ `(3)/(8) = "AD"/"AB"`
⇒ `"AD"/"AB" = (3)/(8)`
Since DB = AB - AD
⇒ DB
= 8 - 3
= 5
Therefore,
AD : DB = 3 : 5
(ii) DE : BC = 3 : 8
Since DE || BC
`"DE"/"BC" = "AE"/"AC"`
⇒ `(3)/(8) = "AE"/(16)`
⇒ AE = `(3 xx 16)/(8)`
⇒ AE = 6.
APPEARS IN
RELATED QUESTIONS
In ΔABC and ΔDEF, it is being given that: AB = 5 cm, BC = 4 cm and CA = 4.2 cm; DE=10cm, EF = 8 cm and FD = 8.4 cm. If AL ⊥ BC and DM ⊥ EF, find AL: DM.
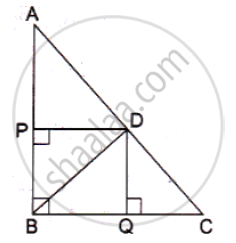
In a right triangle ABC, right angled at B, D is a point on hypotenuse such that BD ⊥ AC , if DP ⊥ AB and DQ ⊥ BC then prove that
`(a) DQ^2 Dp.QC (b) DP ^2 DQ.AP 2 `
In Δ ABC , MN || BC .
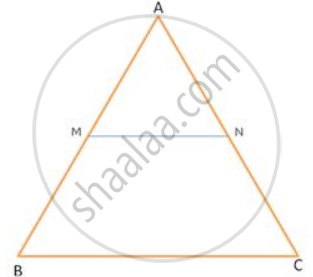
If BC = 14 cm and MN = 6 cm , find `("Ar" triangle "AMN")/("Ar" . ("trapezium MBCN"))`
In the following figure, point D divides AB in the ratio 3 : 5. Find :
BC = 4.8 cm, find the length of DE.
Prove that the area of the triangle BCE described on one side BC of a square ABCD as base is one half of the area of similar triangle ACF described on the diagonal AC as base.
In the given figure, AB and DE are perpendicular to BC.
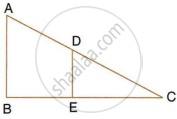
- Prove that ΔABC ∼ ΔDEC
- If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
- Find the ratio of the area of a ΔABC : area of ΔDEC.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 4x - 3, AE = 8x - 7, BD = 3x - 1 and CE = 5x - 3,Find x.
Find the scale factor in each of the following and state the type of size transformation:
Model volume = 200cm3, Actual volume = 8cm3
In a triangle ABC, AB = 4 cm, BC = 4.5 cm and CA = 5 cm. Construct ΔABC. Find the image A'B'C of the ΔABC obtained by enlarging it by a scale factor 2. Measure the sides of the image A'B'C' and show that AB:A'B' = AC:B'C' = CA:C'A'
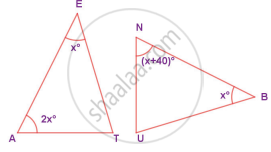
In the given figure, if ΔEAT ~ ΔBUN, find the measure of all angles.