Advertisements
Advertisements
Question
In an adiabatic expansion of the air, the volume is increased by 4%, what is the percentage change in pressure? (For air γ = 1.4)
Solution
From the equation for the adiabatic process,
PVγ = constant
Using differentiation, we get
Pγ Vγ − 1 dV + dP.Vγ = 0
`"dP"/"P" = -γ "dV"/"V"`
Volume 'V' is increased by 4% and γ = 1.4
`"dP"/"P" xx 100 = -γ ("dV"/"V" xx 100)`
= − 1.4 × 4
= − 5.6
Pressure is decreased by 5.6%
APPEARS IN
RELATED QUESTIONS
Explain graphically (i) positive work with varying pressure, (ii) negative work with varying pressure, and (iii) positive work at constant pressure.
When food is cooked in a vessel by keeping the lid closed, after some time the steam pushes the lid outward. By considering the steam as a thermodynamic system, then in the cooking process
The V-T diagram of an ideal gas which goes through a reversible cycle A→B→C→D is shown below. (Processes D→A and B→C are adiabatic)
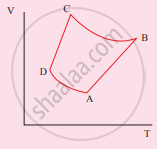
The corresponding PV diagram for the process is (all figures are schematic)
In an isochoric process, we have ____________.
Give an expression for work done in an isothermal process.
Give the equation of state for an adiabatic process.
Derive the work done in an adiabatic process.
Among the amount of heat absorbed and the amount of work done by a system, ______
Two identical samples of a gas are allowed to expand (i) isothermally (ii) adiabatically. Work done is ____________.
Assertion: Equal volumes of monatomic and polyatomic gases are adiabatically compressed separately to equal compression ratio `("P"_2/"P"_1)`. Then monatomic gas will have greater final volume.
Reason: Among ideal gases, molecules of a monatomic gas have the smallest number of degrees of freedom.
