Advertisements
Advertisements
Question
Derive the work done in an adiabatic process.
Solution
Work done in an adiabatic process: Consider µ moles of an ideal gas enclosed in a cylinder having perfectly non-conducting walls and base. A frictionless and insulating piston of cross-sectional area A is fitted in the cylinder.
Let W be the work done when the system goes from the initial state (Pi, Vi, Ti) to the final state (Pf, Vf, Tf) adiabatically.
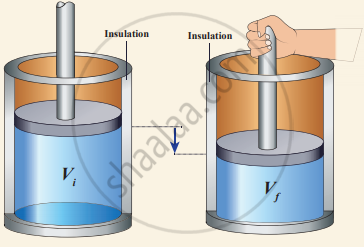
Work done in an adiabatic process
W = `int_("V"_"i")^("V"_"f") "PdV"` ..........(1)
By assuming that the adiabatic process occurs quasi-statically, at every stage the ideal gas law is valid. Under this condition, the adiabatic equation of state is PVγ = constant (or)
P = `"constant"/"V"^γ` can be substituted in the equation (1), we get
∴ Wadia = `int_("V"_"i")^("V"_"f") "constant"/"V"^γ "dV" = "constant" int_("V"_"i")^("V"_"f") "V"^-γ "dV"`
= `"constant" [("V"^(-γ + 1))/(-γ + 1)]_("V"_"i")^("V"_"f") = "constant"/(1 - γ) [1/("V"_"f"^(γ - 1)) - 1/("V"_"i"^(γ - 1))]`
= `1/(1 - γ) ["constant"/("V"_"f"^(γ - 1)) - "constant"/("V"_"i"^(γ - 1))]`
But, `"P"_"i""V"_"i"^γ = "P"_"f""V"_"f"^γ = "constant"`
∴ Wadia = `1/(1 - γ) [("P"_"f""V"_"f"^γ)/("V"_"f"^(γ - 1)) - ("P"_"i""V"_"i"^γ)/("V"_"i"^(γ - 1))]`
Wadia = `1/(1 - γ) ["P"_"f""V"_"f" - "P"_"i""V"_"i"]` .......(2)
From ideal gas law, PfVf = μRTf and PiVi = μRTi
Substituting in equation (2), we get
∴ Wadia = `(μ"R")/(γ - 1) ["T"_"i" - "T"_"f"]` ..........(3)
In adiabatic expansion, work is done by the gas. i.e., Wadia is positive. As Ti > Tf the gas cools during adiabatic expansion.
In adiabatic compression, work is done on the gas. i.e., Wadia is negative. As Ti < Tf the temperature of the gas increases during adiabatic compression.


PV diagram - Work done in the adiabatic process
To differentiate between isothermal and adiabatic curves in the PV diagram, the adiabatic curve is drawn along with the isothermal curve for Tf and Ti. Note that the adiabatic curve is steeper than an isothermal curve. This is because γ > 1 always.
APPEARS IN
RELATED QUESTIONS
A thermodynamic system is taken from an original state to an intermediate state by the linear process shown in Figure

Its volume is then reduced to the original value from E to F by an isobaric process. Calculate the total work done by the gas from D to E to F
Draw a p-V diagram showing negative work with varying pressure.
Differentiate between the reversible and irreversible processes.
Explain work done during a thermodynamic process.
When you exercise in the morning, by considering your body as a thermodynamic system, which of the following is true?
Draw the PV diagram for the isobaric process.
What is a cyclic process?
Explain in detail an adiabatic process.
An ideal gas is made to go from a state A to stale B in the given two different ways (see figure) (i) an isobaric and then an isochoric process and (ii) an isochoric and then an isobaric process. The work done by gas in the two processes are W1 and W2 respectively. Then,

An ideal gas is compressed to half its initial volume by means of several processes. Which of the process results in the maximum work done on the gas?
