Advertisements
Advertisements
Question
Explain the isobaric process and derive the work done in this process.
Solution
Isobaric process: This is a thermodynamic process that occurs at constant pressure. Even though the pressure is constant in this process, temperature, volume and internal energy are not constant. From the ideal gas equation, we have
V = `((μ"R")/"P")"T"` .........(1)
Here, `(μ"R")/"P"` = constant
In an isobaric process the temperature is directly proportional to volume.
V ∝ T (Isobaric process) …........(2)
This implies that for an isobaric process, the V-T graph is a straight line passing through the origin.
If gas goes from a state (Vi, Ti) to (Vf, Tf) at constant pressure, then the system satisfies the following equation
`"T"_"f"/"V"_"f" = "T"_"i"/"V"_"i"` ...........(3)
Examples for Isobaric process:
(i) When the gas is heated and pushes the piston so that it exerts a force equivalent to atmospheric pressure plus the force due to gravity then this process is isobaric.
(ii) Most of the cooking processes in our kitchen are isobaric processes. When the food is cooked in an open vessel, the pressure above the food is always at atmospheric pressure. The PV diagram for an isobaric process is a horizontal line parallel to the volume axis. Figure (a) represents the isobaric process where volume decreases figure
(b) represents the isobaric process where volume increases.

PV diagram for an isobaric process
The work done in an isobaric process: Work done by the gas
W = `int_("V"_"i")^("V"_"f") "PdV"` ..........(4)
In an isobaric process, the pressure is constant, so P comes out of the integral,
W = `"P" int_("V"_"i")^("V"_"f") "dV"` ........(5)
W = P[Vf – Vi] = PΔV ........(6)
Where ∆V denotes the change in the volume. If ∆V is negative, W is also negative. This implies that the work is done on the gas. If ∆V is positive, W is also positive, implying that work is done by the gas equation.
The equation (6) can also be rewritten using the ideal gas equation.
From ideal gas equation
PV = μRT and V = `(μ"RT")/"P"`
Substituting this in equation (6) we get
W = `μ"RT"_"f" (1 - "T"_"i"/"T"_"f")` ...........(7)
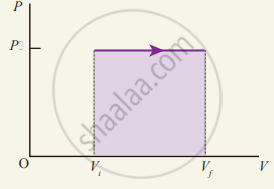
Work done in an isobaric process
In the PV diagram, the area under the isobaric curve is equal to the work done in the isobaric process. The shaded area in the above diagram is equal to the work done by the gas.
The first law of thermodynamics for the isobaric process is given by
ΔU = Q − PΔV ......(8)
W = PΔV, ΔU = `"Q" - μ"RT"_"f" [1 - "T"_"i"/"T"_"f"]`
APPEARS IN
RELATED QUESTIONS
Draw a p-V diagram showing negative work with varying pressure.
3 mole of a gas at temperature 400 K expands isothermally from an initial volume of 4 litres to a final volume of 8 litres. Find the work done by the gas. (R = 8.31 J mol-1 K-1)
Explain graphically (i) positive work with varying pressure, (ii) negative work with varying pressure, and (iii) positive work at constant pressure.
Give the equation of state for an isothermal process.
Draw the PV diagram for the isobaric process.
What is meant by a reversible and irreversible processes?
Explain in detail the isochoric process.
Among the amount of heat absorbed and the amount of work done by a system, ______
An ideal gas is made to go from a state A to stale B in the given two different ways (see figure) (i) an isobaric and then an isochoric process and (ii) an isochoric and then an isobaric process. The work done by gas in the two processes are W1 and W2 respectively. Then,

Explain the thermodynamic process.
