Advertisements
Advertisements
Question
In the following, one of the six trigonometric ratios is given. Find the values of the other trigonometric ratios.
`tan alpha = 5/12`
Solution
`tan alpha = 5/12`
We know that `tan alpha ="opposite side/adjacent side"= 5/12`
Now consider a right-angled Δle ABC
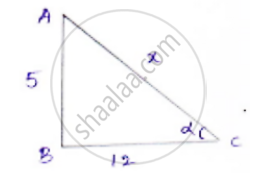
Let x = hypotenuse .By applying Pythagoras theorem
𝐴𝐶2 = 𝐴𝐵2 + 𝐵𝐶2
𝑥2 = 52 + 122
𝑥2 = 25 + 144 = 169
𝑥 = 13
`sin α = "adjacent side"/"hypotenuse"= 5/13`
`cos α = "adjacent side"/"hypotenuse" = 12/13`
cot α = `1/tan alpha = 12/15``
cosec α = `1/sin alpha = (1/5)/13 = 13/5`
sec α = `1/cos alpha = (1/12)/13 = 13/12`
APPEARS IN
RELATED QUESTIONS
In the following, trigonometric ratios are given. Find the values of the other trigonometric ratios.
`cos A = 4/5`
In the following, one of the six trigonometric ratios is given. Find the values of the other trigonometric ratios.
tan θ = 11
if `tan theta = 12/13` Find `(2 sin theta cos theta)/(cos^2 theta - sin^2 theta)`
Evaluate the following
cos2 30° + cos2 45° + cos2 60° + cos2 90°
Evaluate the following
`2 sin^2 30^2 - 3 cos^2 45^2 + tan^2 60^@`
Evaluate the following:
(cosec2 45° sec2 30°)(sin2 30° + 4 cot2 45° − sec2 60°)
Find the value of x in the following :
`sqrt3 sin x = cos x`
In ΔABC is a right triangle such that ∠C = 90° ∠A = 45°, BC = 7 units find ∠B, AB and AC
If `sqrt2 sin (60° – α) = 1` then α is ______.
Prove the following:
If tan A = `3/4`, then sinA cosA = `12/25`
