Advertisements
Advertisements
Question
Evaluate the following:
(cosec2 45° sec2 30°)(sin2 30° + 4 cot2 45° − sec2 60°)
Solution
Given,
(cosec2 45° sec2 30°)(sin2 30° + 4 cot2 45° − sec2 60°) …(i)
= `((sqrt2)^2 · (2/sqrt3)^2)((1/2)^2 + 4(1)^2 - (2)^2)`
= `(8/3)(1/4 + 4 - 4)`
= `8/3·1/4`
= `2/3`
APPEARS IN
RELATED QUESTIONS
State whether the following are true or false. Justify your answer.
sec A = `12/5` for some value of angle A.
If sec θ = `13/5, "show that" (2sinθ - 3 cosθ)/(4sinθ - 9cosθ) = 3`.
if `sin theta = 3/4` prove that `sqrt(cosec^2 theta - cot)/(sec^2 theta - 1) = sqrt7/3`
`(sin theta)/(1 + cos theta)` is ______.
The value of cos 0°. cos 1°. cos 2°. cos 3°… cos 89° cos 90° is ______.
Prove that sec θ + tan θ = `cos θ/(1 - sin θ)`.
Proof: L.H.S. = sec θ + tan θ
= `1/square + square/square`
= `square/square` ......`(∵ sec θ = 1/square, tan θ = square/square)`
= `((1 + sin θ) square)/(cos θ square)` ......[Multiplying `square` with the numerator and denominator]
= `(1^2 - square)/(cos θ square)`
= `square/(cos θ square)`
= `cos θ/(1 - sin θ)` = R.H.S.
∴ L.H.S. = R.H.S.
∴ sec θ + tan θ = `cos θ/(1 - sin θ)`
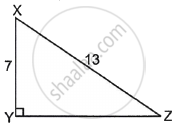
In the given figure, if sin θ = `7/13`, which angle will be θ?
Find an acute angle θ when `(cos θ - sin θ)/(cos θ + sin θ) = (1 - sqrt(3))/(1 + sqrt(3))`
If sinθ = `1/sqrt(2)` and `π/2 < θ < π`. Then the value of `(sinθ + cosθ)/tanθ` is ______.
Evaluate 2 sec2 θ + 3 cosec2 θ – 2 sin θ cos θ if θ = 45°.
