Advertisements
Advertisements
Question
if `sin theta = 3/4` prove that `sqrt(cosec^2 theta - cot)/(sec^2 theta - 1) = sqrt7/3`
Advertisements
Solution
We have `sin theta = 3/4`
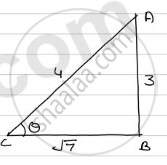
In ΔABC
`AC^2 = AB^2 + BC^2`
`=> (4)^2 = (3)^2 + BC^2`
`=> BC^2= 16 - 9`
`=> BC^2 = 7`
`=> BC = sqrt7`
`:. cosec theta = 4/3, sec theta = 4/sqrt7 and cot theta = sqrt7/3`
Now
L.H.S `sqrt((cosec^2 theta - cot^2 theta)/(sec^2 theta - 1))`
`= sqrt(((4/3)^2 - (sqrt7/3)^2)/((4/sqrt7)^2 - 1)`
`= sqrt((16/9 - 7/9)/(16/7 - 1)`
`=sqrt((9/9)/((16 - 7)/7 ))`
`= sqrt(7/9)`
`= sqrt7/3`
= R.H.S
APPEARS IN
RELATED QUESTIONS
If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
State whether the following are true or false. Justify your answer.
cos A is the abbreviation used for the cosecant of angle A.
In the following, trigonometric ratios are given. Find the values of the other trigonometric ratios.
`sin A = 2/3`
In the following, one of the six trigonometric ratios is given. Find the values of the other trigonometric ratios.
`tan alpha = 5/12`
In the following, trigonometric ratios are given. Find the values of the other trigonometric ratios.
`cos theta = 7/25`
In the following, trigonometric ratios are given. Find the values of the other trigonometric ratios.
`sec theta = 13/5`
If `sec θ = 13/5`, show that `(2 sin θ - 3 cos θ)/(4 sin θ - 9 cos θ) = 3`.
if `tan theta = 12/13` Find `(2 sin theta cos theta)/(cos^2 theta - sin^2 theta)`
Evaluate the Following
4(sin4 60° + cos4 30°) − 3(tan2 60° − tan2 45°) + 5 cos2 45°
In ΔABC is a right triangle such that ∠C = 90° ∠A = 45°, BC = 7 units find ∠B, AB and AC
sin (45° + θ) – cos (45° – θ) is equal to ______.
If A and (2A – 45°) are acute angles such that sin A = cos (2A – 45°), then tan A is equal to ______.
If cos A = `4/5`, then the value of tan A is ______.
If sin A = `1/2`, then the value of cot A is ______.
Given that sinα = `1/2` and cosβ = `1/2`, then the value of (α + β) is ______.
Find the value of sin 0° + cos 0° + tan 0° + sec 0°.
What will be the value of sin 45° + `1/sqrt(2)`?
In the given figure, if sin θ = `7/13`, which angle will be θ?
If f(x) = `3cos(x + (5π)/6) - 5sinx + 2`, then maximum value of f(x) is ______.
If θ is an acute angle of a right angled triangle, then which of the following equation is not true?
