Question

In the parabola y² = 4ax, the length of the chord passing through the vertex and inclined to the axis at π/4 is

Options

• \[4\sqrt{2}a\] 

• \[2\sqrt{2}a\]

• \[\sqrt{2}a\] 

• none of these 

Answer 1

\[4\sqrt{2}a\] 

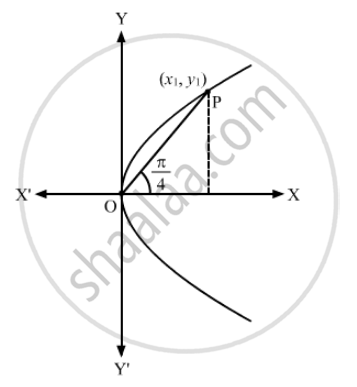
Let OP be the chord.
Let the coordinates of P be \[\left( x_1 , y_1 \right)\] 

From the figure, we have: 

\[O P^2 = {x_1}^2 + {y_1}^2\]         (1) 

And, 

\[\tan\frac{\pi}{4} = \frac{y_1}{x_1}\] 

\[\Rightarrow x_1 = y_1\]                  (2) 

Also, 

\[\left( x_1 , y_1 \right)\]  lies on the parabola. 

∴ \[{y_1}^2 = 4a x_1\]                           (3) 

Using (2) and (3): 

\[{x_1}^2 = 4a x_1 \Rightarrow x_1 = 4a\]        (4)

∴ From (4), (1) and (2), we have:  

\[O P^2 = \left( 4a \right)^2 + \left( 4a \right)^2 = 32 a^2 \]
\[ \Rightarrow OP = 4\sqrt{2}a\] 

Therefore, the length of the chord is \[4\sqrt{2}a \text{ units }\]