Advertisements
Advertisements
Question
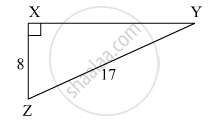
In right angled ΔYXZ, ∠X = 90°, XZ = 8 cm, YZ = 17 cm, find sin Y, cos Y, tan Y, sin Z, cos Z, tan Z.
Solution
In right ∆YXZ,
YZ2 = XZ2 + XY2 ...(Pythagoras theorem)
⇒ XY2 = YZ2 − XZ2
⇒ XY2 = 172 − 82
⇒ XY2 = 289 − 64
⇒ XY2 = 225
⇒ XY2 = 152
∴ XY = 15 cm
Now,
sin Y = `("∠Y" "opposite side")/"Hypotenuse" = "XZ"/"YZ" = 8/17`
cos Y = `("∠Y" "adjacent side")/"Hypotenuse" = "XY"/"YZ" = 15/17`
tan Y = `("∠Y" "opposite side")/("∠Y" "adjacent side") = "XZ"/"XY" = 8/15`
Also,
sin Z = `("∠Z" "opposite side")/"Hypotenuse" = "XY"/"YZ" = 15/17`
cos Z = `("∠Z" "adjacent side")/"Hypotenuse" = "XZ"/"YZ" = 8/17`
tan Z = `("∠Z" "opposite side")/("∠Z" "adjacent side") = "XY"/"XZ" = 15/8`
APPEARS IN
RELATED QUESTIONS
In the given Figure, ∠R is the right angle of ΔPQR. Write the following ratios.
- sin P
- cos Q
- tan P
- tan Q

In the right angled Δ XYZ, ∠XYZ = 90° and a, b, c are the lengths of the sides as shown in the figure. Write the following ratios,
- sin X
- tan Z
- cos X
- tan X.

In right angled ΔLMN, ∠LMN = 90°, ∠L = 50° and ∠N = 40°, write the following ratios.
- sin 50°
- cos 50°
- tan 40°
- cos 40°

In the given figure, ∠PQR = 90°, ∠PQS = 90°, ∠PRQ = α and ∠QPS = θ Write the following trigonometric ratios.
- sin α, cos α, tan α
- sin θ, cos θ, tan θ

In the given figure, `angle` PQR = 90° , `angle` PQS = 90° , `angle` PRQ = θ and `angle` QPS = θ Write the following trigonometric ratios.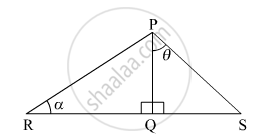
(i) sin θ, cos θ, tan θ
(ii) sin θ , cos θ , tan θ
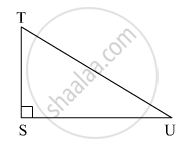
In right angled ΔTSU, TS = 5, ∠S = 90°, SU = 12 then find sin T, cos T, tan T. Similarly find sin U, cos U, tan U.
In right angled ΔLMN, if ∠N =θ, ∠M = 90, cos θ =`24/25`, find sin θ and tan θ Similarly, find (sin2 θ) and (cos2 θ).

