Advertisements
Advertisements
Question
In the following table, a ratio is given in each column. Find the remaining two ratios in the column and complete the table.
| sin θ | `11/61` | `1/2` | `3/5` | ||||||
| cos θ | `35/37` | `1/sqrt3` | |||||||
| tan θ | `1` | `21/20` | `8/15` | `1/(2sqrt2)` |
Solution
| sin θ | `bb(12/37)` | `11/61` | `bb(1/sqrt2)` | `1/2` | `bb(sqrt2/sqrt3)` | `bb(21/29)` | `bb(8/17)` | `3/5` | `bb(1/3)` |
| cos θ | `35/37` | `bb(60/61)` | `bb(1/sqrt2)` | `bb(sqrt3/2)` | `1/sqrt3` | `bb(20/29)` | `bb(15/17)` | `bb(4/5)` | `bb((2sqrt2)/3)` |
| tan θ | `bb(12/35)` | `bb(11/60)` | 1 | `bb(1/sqrt3)` | `bb(sqrt2)` | `21/20` | `8/15` | `bb(3/4)` | `1/(2sqrt2)` |
Explanation:
(i) cos θ = `35/37` ...(i)[Given]
In right angled ΔABC,

∠C = θ
cos θ = `"Adjacent side of θ"/"Hypotenuse"`
∴ cos θ = `"BC"/"AC"` ...(ii)
∴ `"BC"/"AC" = 35/37` ...[From (i) and (ii)]
Let the common multiple be k.
∴ BC = 35k and AC = 37k
Now, AC2 = AB2 + BC2 ...[Pythagoras theorem]
∴ (37k)2 = AB2 + (35k)2
1369k2 = AB2 + 1225k2
AB2 = 1369k2 – 1225k2
AB2 = 144k2
AB2 = (12k)2
Taking square root of both sides,
AB = 12k
∴ sin θ = `"Opposite side of θ"/"Hypotenuse" = "AB"/"AC" = "12k"/"37k" = 12/37`.
tan θ = `"Opposite side of θ"/"Adjacent side of θ" = "AB"/"BC" = "12k"/"35k" = 12/35`.
(ii) sin θ = `11/61` ...(i)[Given]
In right angled ΔABC, ∠C = θ
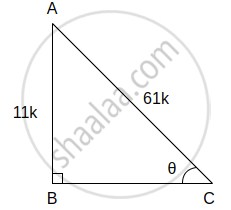
sin θ = `"Opposite side of θ"/"Hypotenuse"`
∴ sin θ = `"AB"/"AC"` ...(ii)
∴ `"AB"/"AC" = 11/61` ...[From (i) and (ii)]
Let the common multiple be k.
AB = 11k and AC = 61k
Now, AC2 = AB2 + BC2 ...[Pythagoras theorem]
∴ (61k)2 = (11k)2 + BC2
∴ 3721k2 = 121k2 + BC2
∴ BC2 = 3721k2 – 121k2
∴ BC2 = 3600k2
∴ BC2 = (60k)2
Taking square root of both sides,
BC = 60k
∴ cos θ = `"Adjacent side of θ"/"Hypotenuse" = "BC"/"AC" = "60k"/"61k" = 60/61`
tan θ = `"Opposite side of θ"/"Adjacent side of θ" = "AB"/"BC" = "11k"/"60k" = 11/60`.
(iii) tan θ = 1 ...(i) [Given]
In right angled ∆ABC, ∠C = θ

tan θ = `"Opposite side of θ"/"Adjacent side of θ"`
∴ tan θ = `"AB"/"BC"` ...(ii)
∴ `"AB"/"BC" = 1/1` ...[From (i) and (ii)]
Let the common multiple be k.
∴ AB = 1k and BC = 1k
Now, AC2 = AB2 + BC2 ...[Pythagoras theorem]
∴ AC2 = k2 + k2
∴ AC2 = 2k2
Taking square root of both sides,
∴ AC = `sqrt2k`
∴ sin θ = `"Opposite side of θ"/"Hypotenuse" = "AB"/"AC" = "1k"/(sqrt2"k") = 1/sqrt2`
∴ cos θ = `"Adjacent side of θ"/"Hypotenuse" = "BC"/"AC" = "1k"/(sqrt2"k") = 1/sqrt2`
(iv) sin θ = `1/2` ...(i)[Given]
In right angled ∆ABC, ∠C = θ
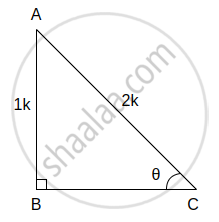
sin θ = `"Opposite side of θ"/"Hypotenuse"`
∴ sin θ = `"AB"/"AC"` ...(ii)
∴ `"AB"/"AC" = 1/2` ...[From (i) and (ii)]
Let the common multiple be k.
∴ AB = 1k and AC = 2k
Now, AC2 = AB2 + BC2 ...[Pythagoras theorem]
∴ (2k)2 = k2 + BC2
∴ 4k2 = k2 + BC2
∴ BC2 = 4k2 – k2
∴ BC2 = 3k2
Taking square root of both sides,
∴ BC = `sqrt3"k"`
∴ cos θ = `"Adjacent side of θ"/"Hypotenuse" = "BC"/"AC" = (sqrt3"k")/(2"k") = (sqrt3)/2`
tan θ = `"Opposite side of θ"/"Adjacent side of θ" = "AB"/"BC" = (1"k")/(sqrt3"k") = 1/sqrt3`
(v) cos θ = `1/sqrt3` ...(i)[Given]
In right angled ∆ABC, ∠C = θ
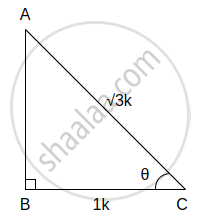
∴ cos θ = `"Adjacent side of θ"/"Hypotenuse"`
∴ cos θ = `"BC"/"AC"` ...(ii)
∴ `"BC"/"AC" = 1/sqrt3` ...[From (i) and (ii)]
Let the common multiple be k.
∴ `"AB" = 1"k" and "BC" = sqrt3"k"`
Now, AC2 = AB2 + BC2 ...[Pythagoras theorem]
`∴ (sqrt3"k")^2 = "AB"^2 + "k"^2`
∴ 3k2 = AB2 – k2
∴ AB2 = 3k2 – k2
∴ AB2 = 2k2
Taking square root of both sides,
AB = `sqrt2`k
∴ sin θ = `"Opposite side of θ"/"Hypotenuse" = "AB"/"AC" = (sqrt2"k")/(sqrt3"k") = sqrt2/sqrt3`
tan θ = `"Opposite side of θ"/"Adjacent side of θ" = "AB"/"BC" = (sqrt2"k")/(1"k") = sqrt2`
(vi) tan θ = `21/20` ...(i)[Given]
In right angled ∆ABC, ∠C = θ
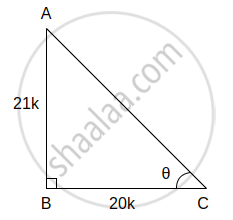
tan θ = `"Opposite side of θ"/"Adjacent side of θ"`
∴ tan θ = `"AB"/"BC"` ...(ii)
∴ `"AB"/"BC" = 21/20` ...[From (i) and (ii)]
Let the common multiple be k.
∴ AB = 21k and BC = 20k
Now, AC2 = AB2 + BC2 ...[Pythagoras theorem]
AC2 = (21k)2 + (20k)2
AC2 = 441k2 + 400k2
AC2 = (841k)2
Taking square root of both sides,
AC = 29k
∴ sin θ = `"Opposite side of θ"/"Hypotenuse" = "AB"/"AC" = (21"k")/(29"k") = 21/29`
cos θ = `"Adjacent side of θ"/"Hypotenuse" = "BC"/"AC" = (20"k")/(29"k") = 20/29`
(vii) tan θ = `8/15` ...(i)[Given]
In right angled ∆ABC, ∠C = θ.

tan θ = `"Opposite side of θ"/"Adjacent side of θ"`
∴ tan θ = `"AB"/"BC"` ...(ii)
∴ `"AB"/"BC" = 8/15` ...[From (i) and (ii)]
Let the common multiple be k.
∴ AB = 8k and BC = 15k
Now, AC2 = AB2 + BC2 ...[Pythagoras theorem]
∴ AC2 = (8k)2 + (15k)2
∴ AC2 = 64k2 + 225k2
∴ AC2 = (289k)2
Taking square root of both sides,
∴ AC = 17k
∴ sin θ = `"Opposite side of θ"/"Hypotenuse" = "AB"/"AC" = (8"k")/(17"k") = 8/17`
cos θ = `"Adjacent side of θ"/"Hypotenuse" = "BC"/"AC" = (15"k")/(17"k") = 15/17`
(viii) sin θ = `3/5` ...(i)[Given]
In right angled ΔABC, ∠C = θ
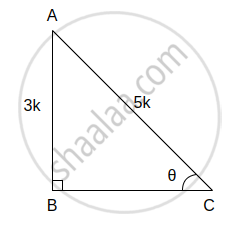
sin θ = `"Opposite side of θ"/"Hypotenuse"`
∴ sin θ = `"AB"/"AC"` ...(ii)
∴ `"AB"/"AC" = 3/5` ...[From (i) and (ii)]
Let the common multiple be k.
∴ AB = 3k and AC = 5k
Now, AC2 = AB2 + BC2 ...[Pythagoras theorem]
∴ (5k)2 = (3k)2 + BC2
∴ 25k2 = 9k2 + BC2
∴ BC2 = 25k2 – 9k2
∴ BC2 = 16k2
Taking square root of both sides,
∴ BC = 4k
∴ cos θ = `"Adjacent side of θ"/"Hypotenuse" = "BC"/"AC" = (4"k")/(5"k") = 4/5`
tan θ = `"Opposite side of θ"/"Adjacent side of θ" = "AB"/"BC" = (3"k")/(4"k") = 3/4`
(ix) tan θ = `1/(2sqrt2)` ...(i)[Given]
In right angled ∆ABC, ∠C = θ
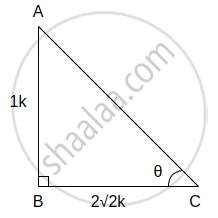
tan θ = `"Opposite side of θ"/"Adjacent side of θ"`
∴ tan θ = `"AB"/"BC"` ...(ii)
∴ `"AB"/"BC" = 1/(2sqrt2)` ...[From (i) and (ii)]
Let the common multiple be k.
∴ AB = 1k and BC = `2sqrt2"k"`
Now, AC2 = AB2 + BC2 ...[Pythagoras theorem]
∴ `"AC"^2 = (1"k")^2 + (2sqrt2"k")^2 `
∴ AC2 = 1k2 + 8k2
∴ AC2 = (9k)2
Taking square root of both sides,
∴ AC = 3k
∴ sin θ = `"Opposite side of θ"/"Hypotenuse" = "AB"/"AC" = (1"k")/(3"k") = 1/3`
cos θ = `"Adjacent side of θ"/"Hypotenuse" = "BC"/"AC" = (2sqrt2"k")/(3"k") = (2sqrt2)/3`
APPEARS IN
RELATED QUESTIONS
Find the value of the following:
cos 74° 39′
Find the value of the following:
tan 54° 26′
Find the value of the following:
cos 33° 53′
Find the value of θ if cos θ = 0.0410
Find the value of θ if tan θ = 7.5958
Find the value of the following:
tan 70° 17′
Find the area of a right triangle whose hypotenuse is 10 cm and one of the acute angle is 24°24′
Find the angle made by a ladder of length 5m with the ground, if one of its end is 4m away from the wall and the other end is on the wall
In the given figure, HT shows the height of a tree standing vertically. From a point P, the angle of elevation of the top of the tree (that is ∠P) measures 42° and the distance to the tree is 60 metres. Find the height of the tree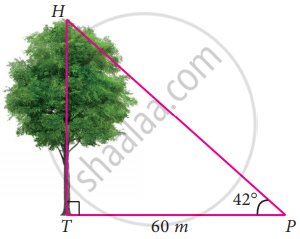
The value of 2tan45° – 2sin30° is ______.
